Cho tam giác ABC cạnh a. Tính độ dài của các vectơ
#Hỏi cộng đồng OLM
#Toán lớp 10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

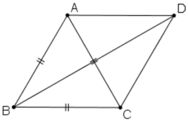
Ta có:
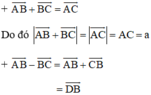
(Quy tắc hình bình hành)
(Trong đó D là đỉnh còn lại của hình bình hành ABCD)
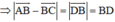
+ Tính BD:
Hình bình hành ABCD có AB = BC = a nên ABCD là hình thoi.
⇒ AC ⊥ BD tại O là trung điểm của AC và BD.
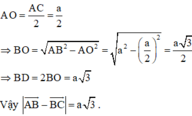

Các vectơ có độ dài bằng a và có điểm đầu, điểm cuối là các đỉnh của tam giác ABC là:
\(\overrightarrow {AB} ;\;\overrightarrow {BA} ;\;\overrightarrow {AC} ;\;\overrightarrow {CA} ;\;\overrightarrow {BC} ;\;\overrightarrow {CB} \)
Chú ý khi giải:
Vectơ \(\overrightarrow {AB} \) khác vectơ \(\overrightarrow {BA} \) (khác nhau điểm đầu và điểm cuối).

Tham khảo:
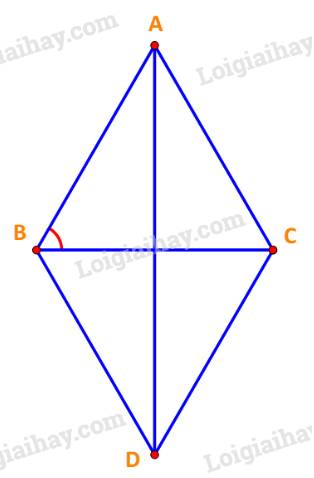
\(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \Rightarrow \left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} } \right| = CB = a.\)
Dựng hình bình hành ABDC tâm O như hình vẽ.
Ta có:
\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \)
\( \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD\)
Vì tứ giác ABDC là hình bình hành, lại có \(AB = AC = BD = CD = a\) nên ABDC là hình thoi.
\( \Rightarrow AD = 2AO = 2.AB.\sin B = 2a.\frac{{\sqrt 3 }}{2} = a\sqrt 3 .\)
Vậy \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| = a\) và \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3 \).

Gọi O là trung điểm của AM
BM=BC/2=a/2
\(\Leftrightarrow AM=\dfrac{a\sqrt{3}}{2}\)
\(\Leftrightarrow MO=\dfrac{a\sqrt{3}}{4}\)
Xét ΔOMB vuông tại M có
\(BO^2=OM^2+BM^2\)
\(=a^2\cdot\dfrac{3}{16}+a^2\cdot\dfrac{1}{4}=a^2\cdot\dfrac{7}{16}\)
\(\Leftrightarrow BO=\dfrac{a\sqrt{7}}{4}\)
Xét ΔBMA có BO là đường trung tuyến
nên \(\overrightarrow{BM}+\overrightarrow{BA}=2\cdot\overrightarrow{BO}\)
\(\Leftrightarrow\left|\overrightarrow{BM}+\overrightarrow{BA}\right|=\dfrac{a\sqrt{7}}{2}\)

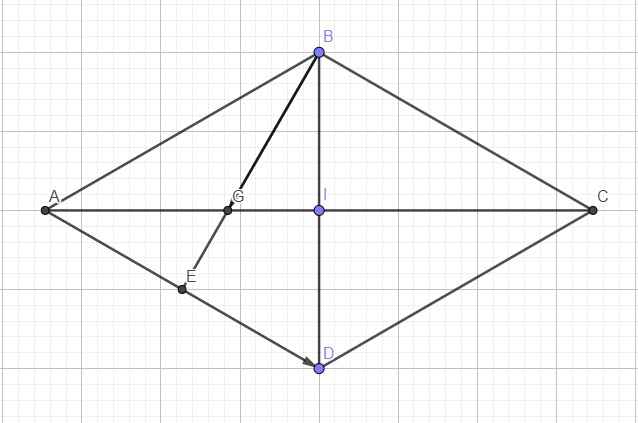
Dựng điểm D sao cho H là trung điểm AD.
Ta có; H là trung điểm của mỗi đường AD ; BC. Do đó, tứ giác ACDB là hình bình hành.
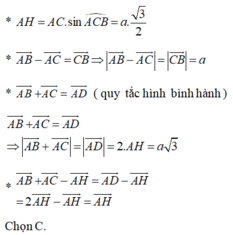

\(\widehat{ABC}=120^0\Rightarrow\widehat{DAB}=180^0-120^0=60^0\)
\(\Rightarrow\Delta ABD\) đều
Gọi E là trung điểm AD \(\Rightarrow\overrightarrow{BE}=\dfrac{1}{2}\overrightarrow{BD}+\dfrac{1}{2}\overrightarrow{BA}\)
\(\Rightarrow\overrightarrow{BG}=\dfrac{2}{3}\overrightarrow{BE}=\dfrac{1}{3}\overrightarrow{BD}+\dfrac{1}{3}\overrightarrow{BA}\)
\(\Rightarrow\overrightarrow{BG}+\overrightarrow{AD}=\dfrac{1}{3}\overrightarrow{BD}+\dfrac{1}{3}\overrightarrow{BA}+\overrightarrow{AD}=\dfrac{1}{3}\left(\overrightarrow{BA}+\overrightarrow{AD}\right)+\dfrac{1}{3}\overrightarrow{BA}+\overrightarrow{AD}\)
\(=\dfrac{2}{3}\overrightarrow{BA}+\dfrac{4}{3}\overrightarrow{AD}=-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{4}{3}\overrightarrow{AD}\)
Đặt \(\overrightarrow{u}=\overrightarrow{BG}+\overrightarrow{AD}\Rightarrow\left|\overrightarrow{u}\right|^2=\left(-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{4}{3}\overrightarrow{AD}\right)=\dfrac{4}{9}AB^2+\dfrac{16}{9}AD^2-\dfrac{16}{9}\overrightarrow{AB}.\overrightarrow{AD}\)
\(=\dfrac{4}{9}.4a^2+\dfrac{16}{9}4a^2-\dfrac{16}{9}.2a.2a.cos60^0=\dfrac{16}{3}a^2\)
\(\Rightarrow\left|\overrightarrow{u}\right|=\dfrac{4a\sqrt{3}}{3}\)

Dựng hình bình hành ABDC.
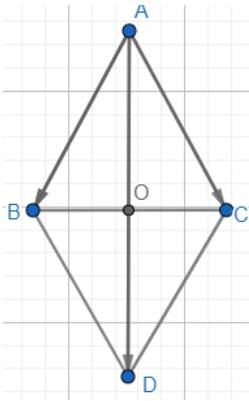
Áp dụng quy tắc hình bình hành vào ABDC ta có:
\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD\)
Gọi O là giao điểm của AD và BC, ta có:
\(AO = \sqrt {A{B^2} - B{O^2}} = \sqrt {A{B^2} - {{\left( {\frac{1}{2}BC} \right)}^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
\(AD = 2AO = a\sqrt 3 \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3 \)
Vậy độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \) là \(a\sqrt 3 \)
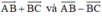
Ta có +
+ 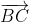 =
= 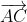
Ta có: –
– 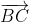 =
=  +
+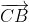 .
.
Trên tia CB, ta dựng =
= 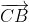
=> –
– 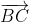 =
=  +
+ =
= 
Tam giác EAC vuông tại A và có : AC = a, CE = 2a , suy ra AE = a√3
Vậy =
=  = a√3
= a√3