Cho tứ giác ABCD. M và N lần lượt là trung điểm của BC và AD. AM cắt BN ở I; DM cắt CN ở J. Chứng minh rằng: SMINJ = SABI + SCDJ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 5 2017
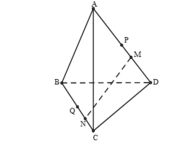
+) Do AM = 3MD; BN = 3NC suy ra:
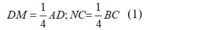
+) Do P và Q lần lượt là trung điểm của AD và BC nên :
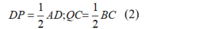
- Từ (1) và (2) suy ra: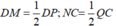 
- Suy ra: M là trung điểm của DP; N là trung điểm CQ.
+) Ta có:
16 tháng 9 2017
Ben 10 làm sai rồi hình như lạc đề luôn đè bài là hình tứ giác sao xuống làm tam giác
21 tháng 9
Sửa đề: Cho hình thang ABCD có AB//CD
a: Xét ΔADC có OM//DC
nên \(\frac{AM}{AD}=\frac{AO}{AC}\left(1\right)\)
Xét ΔBAC có ON//AB
nên \(\frac{OC}{OA}=\frac{CN}{NB}\)
=>\(\frac{AO}{OC}=\frac{BN}{NC}\)
=>\(\frac{AO}{OC+OA}=\frac{BN}{BN+NC}\)
=>\(\frac{AO}{AC}=\frac{BN}{BC}\left(2\right)\)
Từ (1),(2) suy ra \(\frac{AM}{AD}=\frac{BN}{BC}\)
b: Xét tứ giác DMOE có
MO//DE
OE//MD
Do đó: DMOE là hình bình hành
=>DM=OE; DE=OM
Xét ΔADC có MO//DC
nên \(\frac{MO}{DC}=\frac{AM}{AD}\)
c: Xét ΔBDC có ON//DC
nên \(\frac{ON}{DC}=\frac{BN}{BC}\)
mà \(\frac{MO}{DC}=\frac{AM}{AD}\)
và \(\frac{BN}{BC}=\frac{AM}{AD}\)
nên OM=ON(1)
Xét tứ giác FCNO có
FC//NO
FO//NC
Do đó: FCNO là hình bình hành
=>FC=ON(2)
Từ (1),(2) suy ra FC=OM
mà OM=DE
nên FC=DE
d: Xét ΔDAB có OM//AB
nên \(\frac{OM}{AB}=\frac{DM}{DA}\)
Xét ΔADC có OM//DC
nên \(\frac{OM}{DC}=\frac{AM}{AD}\)
\(\frac{OM}{AB}+\frac{OM}{DC}=\frac{DM}{DA}+\frac{AM}{AD}=1\)
=>\(OM\left(\frac{1}{AB}+\frac{1}{DC}\right)=1\)
=>\(\frac{1}{AB}+\frac{1}{DC}=\frac{1}{OM}=\frac{2}{MN}\)
A A K L N F D B M C I J
Giải
SMINJ = SAMD - (SAIN + SDNJ) (1)
Nhưng SAIN = SABN - SABI (2)
Và SDNJ = SNCD - SCJD (3)
Từ (1), (2), (3) \(\Rightarrow\) SMINJ = SAMD + SABI + SCDJ - (SABN + SNCD)
Mặt khác, nếu từ B, M, C hạ các đường vuông góc xuống AD ta được:
ML = \(\dfrac{BK+FC}{2}\) (định lí đường trung bình trong hình thang)
SAMD = \(\dfrac{1}{2}\)AD . ML = \(\dfrac{1}{2}\)AD . \(\left(\dfrac{BK+FC}{2}\right)\)
= SABH + SNCD
Vậy SMINJ = SABI + SCDJ (đpcm)