Diện tích hình phẳng giới hạn bởi các đường cong y = sin x; y= cos x và các đường thẳng bằng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 4 2021
Phương trình hoành độ giao điểm:
\(x^2+1=x+3\Leftrightarrow x^2-x-2=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
\(S=\int\limits^2_{-1}\left|x^2-x-2\right|dx=\int\limits^2_{-1}\left(-x^2+x+2\right)dx=\left(-\dfrac{1}{3}x^3+\dfrac{1}{2}x^2+2x\right)|^2_{-1}=\dfrac{9}{2}\)

CM
23 tháng 3 2018

Chọn C.
Gọi S là diện tích của miền cần tính. Từ hình vẽ và do tính đối xứng ta có


AH
Akai Haruma
Giáo viên
23 tháng 2 2021
Lời giải:
Trước tiên ta tìm giao điểm của 2 ĐTHS:
PT hoành độ giao điểm: $|x^2-4x+3|=x+3$
$\Rightarrow x=0$ hoặc $x=5$
Diện tích hình phẳng giới hạn bởi $(C)$ và $(d)$ là:
\(\int ^5_0(x+3-|x^2-4x+3|)dx=\frac{109}{6}\) (đơn vị diện tích)


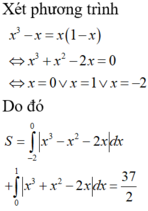



Đáp án C
Giải phương trình: s inx = cos x ⇒ x = π 4 (vì 0 ≤ x ≤ π )
S = ∫ 0 π s inx − cos x d x = 2 2