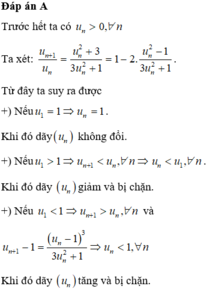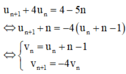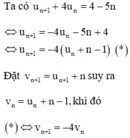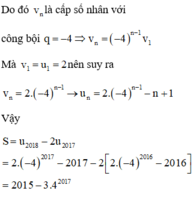Cho dãy số (un) xác định như sau: u1= 2; un+1 - un - 2 + 2(4un+1 - \(\sqrt{4u_n+1}\)) = 0, ∀n∈ N*. Tìm số hạng tổng quát un của dãy số trên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$\frac{u_{n-1}}{u_n}=\frac{n^2}{n^2-1}>0$ với mọi $n\geq 2$ nên $u_{n-1}, u_n$ luôn cùng dấu.
Mà $u_1=2017>0$ nên $u_n>0$ với mọi $n=1,2,...$
Mặt khác:
$n^2(u_{n-1}-u_n)=u_{n-1}>0\Rightarrow u_{n-1}>u_n$ nên dãy $(u_n)$ là dãy giảm.
Dãy giảm và bị chặn dưới nên $u_n$ hội tụ. Đặt $\lim u_n=a$.
Ta có: $a=n^2(a-a)\Rightarrow a=0$
Vậy $\lim u_n=0$

Chọn B.
Ta có: u1 = 1; u2 = 3/2; u3 = 17/6; u4 = 227/34.
Ta chứng minh un > 0 bằng quy nạp.
Giả sử un > 0, khi đó: 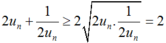
Nên 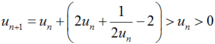 .
.

Chọn A
Phương pháp:
Cách giải: Ta có:
u n + 1 = n = - 4 ( u n + n - 1 )
⇔ u n + 1 + n = - 4 ( u n + n - 1 )
⇔ v n = u n + n - 1 v n + 1 = - 4 v n
Dãy ( v n ) là cấp số nhân với công bội -4 và v 1 = u 1 + 0 = 2
S = u 2018 - 2 u 2017
= v 2018 - 2 v 2017 + 2015
= 2015 - 3 . 4 2017

Đáp án A
Ta có:
u n + 1 + 4 u n = 4 − 5 n ⇔ u n + 1 = − 4 u n − 5 n + 4 ⇔ u n + 1 + n = − 4 u n + n − 1 * .
Đặt v n + 1 = u n + 1 + n suy ra v n = u n + n − 1 , khi đó * ⇔ v n + 1 = − 4 v n
Do đó v n là cấp số nhân với công bội q = − 4 ⇒ v n = − 4 n − 1 v 1
Mà v 1 = u 1 = 2 nên suy ra v n = 2. − 4 n − 1 → u n = 2. − 4 n − 1 − n + 1
Vậy:
S = u 2018 − 2 u 2017 = 2. − 4 2017 − 2017 − 2 2. − 4 2016 − 2016 = 2015 − 3.4 2017 .