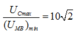Đặt điện áp xoay chiều u = U0cosωt (V) vào hai đầu đoạn mạch AB theo thứ tự gồm điện trở R = 90 Ω; cuộn dây không thuần cảm có r = 10 Ω và tụ điện có điện dung C thay đổi được. M là điểm nối giữa R và cuộn dây. Khi C = C1 thì điện áp hiệu dụng hai đầu đoạn mạch MB đạt giá trị cực tiểu bằng U1. Khi ![]() thì điện áp hiệu dụng trên tụ điện đạt giá trị cực đại bằng U2. Tỉ số
thì điện áp hiệu dụng trên tụ điện đạt giá trị cực đại bằng U2. Tỉ số ![]() bằng:
bằng:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
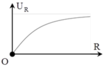
+ Điện áp hiệu dụng hai đầu MB:
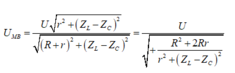
→ Từ phương trình trên, ta thấy rằng, khi ZC1 = ZL thì UMB = UMBmin = U. + Khi C = 0,5C1 → ZC2 = 2ZC1 thì
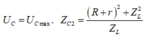
![]()
+ Tỉ số 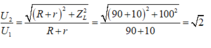

Chuẩn hóa R = r = 1 ⇒ Z L = X Z C = 1 X
Ta có U R C = 3 U d ⇔ 1 2 + 1 X 2 = 3 1 + X 2 ⇒ X = 0 , 528
Hệ số công suất của mạch cos φ = 2 1 2 + X − 1 X 2 ≈ 0 , 83
Đáp án A

Đáp án B
Phương pháp giải: Sử dụng các công thức của bài toán điện dung của tụ điện thay đổi
Điều chỉnh C để điện áp hiệu dụng hai đầu tụ đạt giá trị cực đại thì uRL vuông pha với u
Ta có giản đồ véc tơ như hình bên
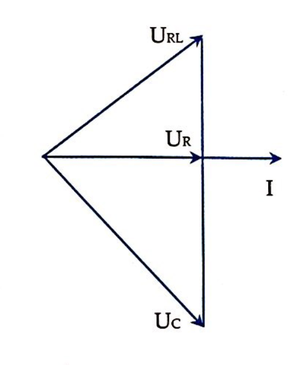
Khi đó u R L 2 U 0 R L 2 + u 2 U 0 2 = 1 ⇔ 50 2 .6 U 0 R L 2 + 150 2 .6 U 0 2 = 1 1
Mặt khác, từ hệ thức lượng trong tam giác vuông ta có:
1 U 0 R L 2 + 1 U 0 2 = 1 U 0 R 2 = 1 150 2 .2 2
Giải (1) và (2) ta thu được U 0 2 = 180000 ⇒ U 0 = 300 2 ⇒ U = 300 V

Đáp án: B
Sử dụng các công thức của bài toán điện dung của tụ điện thay đổi.
Điều chỉnh C để điện áp hiệu dụng hai đầu tụ đạt giá trị cực đại thì uRL vuông pha với u.
Ta có giản đồ véc tơ như hình bên
Khi đó u R L 2 U 0 R L 2 + u 2 U 0 2 = 1 ⇔ 50 2 . 6 U 0 R L 2 + 150 2 . 6 U 0 2 = 1 (1)
Mặt khác, từ hệ thức lượng trong tam giác vuông ta có:
1
U
0
R
L
2
+
1
U
0
2
=
1
U
0
R
2
=
1
150
2
.
2
(2)
Giải (1) và (2) ta thu được U 0 2 = 180000 ⇒ U 0 = 300 2 ⇒ U = 300 (V)

Đáp án B
Phương pháp giải: Sử dụng các công thức của bài toán điện dung của tụ điện thay đổi.
Điều chỉnh C để điện áp hiệu dụng hai đầu tụ đạt giá trị cực đại thì uRL vuông pha với u.
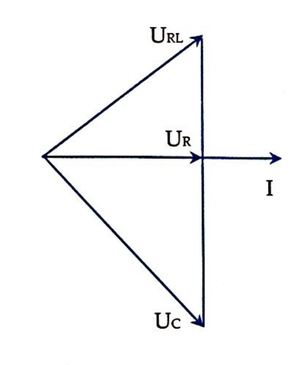


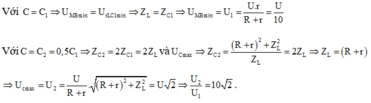
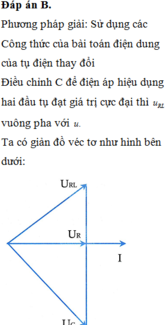

Giải thích: Đáp án C
Ta có: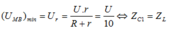
Khi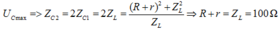
Và có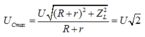
Vậy tỉ số: