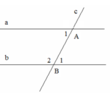
Cho hình vẽ, biết : . Chứng tỏ rằng a//b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

HÌNH TỰ VẼ
TA CÓ :A1+B1=AOB
MÀ A1+600 B2=450
600+450=1050AOB
VẬY AOB=1050

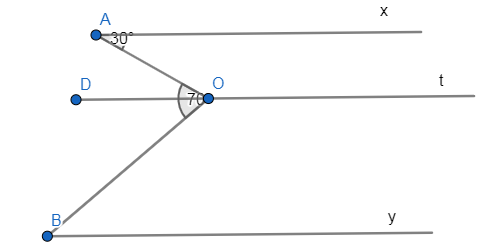
a, Kẻ Ot sao cho Ot song song với Ax và By, ta có:
\(\widehat{xAO}=\widehat{AOD}\) (So le trong)
\(\Rightarrow\widehat{xAO}=\widehat{AOD}=30^0\\\Rightarrow\widehat{DOB}=70^0-30^0=40^0\)
Mà OD//By
\(\Rightarrow\widehat{B}=\widehat{DOB}=40^0\)

Do tam giác ABC vuông nên tổng số đo góc B và C là 1800 - A = 900
Ta có : \(C:B=1:2\)
\(\Rightarrow\dfrac{C}{1}=\dfrac{B}{2}\)
Ấp dụng tính chất dãy tỉ số bằng nhau, ta có :
\(\Rightarrow\dfrac{C}{1}=\dfrac{B}{2}=\dfrac{C+B}{1+2}=\dfrac{90}{3}=30^0\)
\(\Rightarrow\widehat{C}=30.1=30^0\)
\(\Rightarrow\widehat{B}=30.2=60^0\)
Vậy đáp án cần chọn là B

ABCD là hình bình hành
=>AB=CD
=>CD=6(cm)
Diện tích tam giác ADC là:
\(S_{ADC}=\frac12\cdot DA\cdot DC\cdot\sin ADC=\frac12\cdot4\cdot6\cdot\sin60=2\cdot6\cdot\frac{\sqrt3}{2}=6\sqrt3\left(\operatorname{cm}^2\right)\)
ABCD là hình bình hành
=>\(S_{ABCD}=2\cdot S_{ADC}=2\cdot6\sqrt3=12\sqrt3\left(\operatorname{cm}^2\right)\)
Ta có: \(\hat{KAB}+\hat{BAD}=180^0\) (hai góc kề bù)
\(\hat{BAD}+\hat{ADC}=180^0\) (ABCD là hình bình hành)
Do đó: \(\hat{KAB}=\hat{ADC}=60^0\)
Xét ΔKAB vuông tại K có \(\sin KAB=\frac{KB}{AB}\)
=>\(\frac{KB}{6}=\sin60=\frac{\sqrt3}{2}\)
=>\(KB=6\cdot\frac{\sqrt3}{2}=3\sqrt3\left(\operatorname{cm}\right)\)
ΔKAB vuông tại K
=>\(KA^2+KB^2=AB^2\)
=>\(KA^2=6^2-\left(3\sqrt3\right)^2=36-27=9=3^2\)
=>KA=3(cm)
Diện tích tam giác KAB là:
\(S_{KAB}=\frac12\cdot KA\cdot KB=\frac12\cdot3\cdot3\sqrt3=\frac{9\sqrt3}{2}\left(\operatorname{cm}^2\right)\)
Ta có: BC//AD
=>\(\hat{HCB}=\hat{ADC}\) (hai góc đồng vị)
=>\(\hat{HCB}=60^0\)
Xét ΔHBC vuông tại H có \(\sin HCB=\frac{HB}{BC}\)
=>\(\frac{HB}{4}=\sin60=\frac{\sqrt3}{2}\)
=>\(HB=4\cdot\frac{\sqrt3}{2}=2\sqrt3\left(\operatorname{cm}\right)\)
ΔBHC vuông tại H
=>\(HB^2+HC^2=BC^2\)
=>\(HC^2=4^2-\left(2\sqrt3\right)^2=16-12=4=2^2\)
=>HC=2(cm)
ΔBHC vuông tại H
=>\(S_{HBC}=\frac12\cdot HB\cdot HC=\frac12\cdot2\cdot2\sqrt3=2\sqrt3\left(\operatorname{cm}^2\right)\)
Diện tích tứ giác KBHD là:
\(S_{KBHD}=S_{ABCD}+S_{BAK}+S_{BCH}\)
\(=12\sqrt3+\frac{9\sqrt3}{2}+2\sqrt3=14\sqrt3+4,5\sqrt3=18,5\sqrt3\left(\operatorname{cm}^2\right)\)

\(a,\widehat{xAB}+\widehat{xAt}=180^0\left(kề.bù\right)\\ \Rightarrow\widehat{xAB}=180^0-60^0=120^0\\ \Rightarrow\widehat{xAB}=\widehat{yBA}\left(=120^0\right)\)
Mà 2 góc này ở vị trí so le trong nên \(Ax//By\)
\(b,\widehat{yBC}+\widehat{ABC}+\widehat{yBA}=360^0\\ \Rightarrow\widehat{yBC}=360^0-120^0-90^0=150^0\\ \Rightarrow\widehat{yBC}=\widehat{BCz}\left(=150^0\right)\)
Mà 2 góc này ở vị trí so le trong nên \(By//Cz\)

Giải:
a) Ta thấy \(\widehat{A}+\widehat{D}=180^o\) và 2 góc này ở vị trí trong cùng phía nên AB // CD
Vậy AB // CD
b) Ta có: \(\widehat{A}+\widehat{D}+\widehat{C}+\widehat{ABC}=360^o\) ( vì tổng các góc của 1 hình tứ giác bằng \(360^o\) )
\(\Rightarrow120^o+60^o+30^o+\widehat{ABC}=360^o\)
\(\Rightarrow\widehat{ABC}+210^o=360^o\)
\(\Rightarrow\widehat{ABC}=150^o\)
Vì AB // CD nên \(\widehat{C}=\widehat{xBC}=30^o\) ( so le trong )
Vậy \(\widehat{ABC}=150^o,\widehat{xAB}=30^o\)
Ta có: B ^ 1 + B ^ 2 = 180 0 . ( Kề bù), mà B ^ 1 = 1 2 B ^ 2 nªn B ^ 1 = 180 0 : 3 = 60 0
⇒ A ^ 1 = B ^ 1 = 60 0
Do đó a//b ( vì có cặp góc so le trong bằng nhau).