Cho hai điện trở được mắc song song với nhau như sơ đồ hình vẽ. Điện trở tương đương của đoạn mạch là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Điện trở tương đương đoạn mạch :
\(R = R_1 + R_2 + R_3 = 20 + 30 + 40 = 90 (\Omega) \quad\)
b) Hiệu điện thế giữa hai đầu AB :
\(U = IR = 0,2 \cdot 90 = 18 (V) \quad\)
c) Do \(R_1 \; nt \; R_2 \; nt \; R_3\) nên \(I_1 = I_2 = I_3 = I = 0,2 (A) \quad\)
Hiệu điện thế giữa hai đầu mỗi điện trở :
\(U_1 = I_1 R_1 = 0,2 \cdot 20 = 4 (V) \quad\)
\(U_2 = I_2 R_2 = 0,2 \cdot 30 = 6 (V) \quad\)
\(U_3 = I_3 R_3 = 0,2 \cdot 40 = 8 (V) \quad\)

Đáp án: B
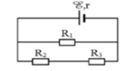
HD Giải: R 23 = 20.30 20 + 30 = 12 Ω , R N = 5 + 12 = 17 Ω I 1 = I = E R N + r = 9 17 + 1 = 0 , 5 A
U1 = R1 I1 = 5.0,5 = 2,5V

Mắc 4 điện trở 20Ω song song với nhau
Ta có: \(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_1}+\dfrac{1}{R_1}+\dfrac{1}{R_1}\)
\(\Leftrightarrow R_{tđ}=\dfrac{R_1R_1R_1R_1}{R_1R_1R_1+R_1R_1R_1+R_1R_1R_1+R_1R_1R_1}\)
\(\Leftrightarrow R_{tđ}=\dfrac{R_1^4}{4R_1^3}=\dfrac{20^4}{4.20^3}=5\left(\Omega\right)\)

a) Điện trở tương đương của mạch đó là:
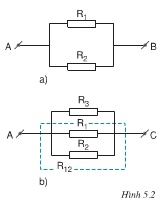
\(R_{12}=\dfrac{R_1R_2}{R_1+R_3}=\dfrac{30.30}{30+30}=\dfrac{900}{60}=15\text{Ω}\)
b) Điện trở tương đương của đoạn mạch mới là
\(R_{td}=\dfrac{R_{12}R_3}{R_{12}+R_3}=\dfrac{15.30}{15+30}=\dfrac{30}{3}=10\text{Ω}\)
+ Điện trở tương đương này luôn nhỏ hơn mỗi điện trở thành phần.

\(R=\rho\dfrac{l}{S}=0,4.10^{-6}.\dfrac{20}{1.10^{-6}}=8\left(\Omega\right)\)
=> Chọn C


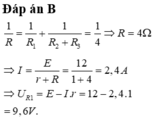
Đáp án B
Điện trở tương đương: R = R 1 . R 2 / ( R 1 + R 2 ) = ( 30 . 20 ) / 50 = 12 Ω
c