Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
Gọi x, y lần lượt là số nhân viên ca I và ca II (x>0,y>0)
Theo giả thiết ta có: \(\left\{ \begin{array}{l}x \ge 6\\x + y \ge 24\\\left( {x + y} \right) - x \le 20\\y \ge 2x\end{array} \right.\)
Biểu diễn tập nghiệm của hệ bất phương trình:
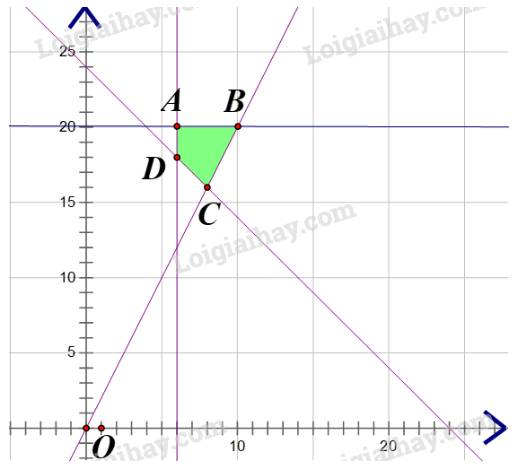
Tập nghiệm của bất phương trình giới hạn bởi tứ giác ABCD với:
\(A(6;20), B(10;20), C(8;16), D(6;18)\)
Tiền lương mỗi ngày của các nhân viên: \(T = 20x + 22y\)(nghìn đồng)
\(T(6;20)=20.6+20.22=560\) (nghìn đồng)
\(T(10;20)=20.10+22.20=640\) (nghìn đồng)
\(T(8;16)=20.8+22.16=512\) (nghìn đồng)
\(T(6;18)=20.6+22.18=516\) (nghìn đồng)
Vậy để tiền lương mỗi ngày ít nhất thì ca I có 8 nhân viên, ca II có 16 nhân viên.

câu trả lời là: Giải......:................................................................................................................................................................................................................................................................................:................................................................................................................................................................................................................................................................................:................................................................................................................................................................................................................................................................................:................................................................................................................................................................................................................................................................................:................................................................................................................................................................................................................................................................................:................................................................................................................................................................................................................................................................................:................................................................................................................................................................................................................................................................................:..........................................................................................................................................................................................................................................................................mik ko bt sorry bạn

Tham khảo:
Gọi x, y lần lượt là số giờ đạp xe và tập tạ trong một tuần.
Ta có các điều kiện ràng buộc đối với x, y như sau:
- Hiển nhiên \(x \ge 0,y \ge 0\)
- Số giờ tập thể dục tối đa là 12 giờ nên \(x + y \le 12\)
- Tổng số calo tiêu hao một tuần không quá 7000 calo nên \(350x + 700y \le 7000\)
Từ đó ta có hệ bất phương trình: \(\left\{ \begin{array}{l}x + y \le 12\\350x + 700y \le 7000\\x \ge 0\\y \ge 0\end{array} \right.\)
Biểu diễn từng miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy, ta được như hình dưới.

Miền không gạch chéo (miền tứ giác OABC, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình.
Với các đỉnh \(O(0;0),\)\(A(0;10),\)\(B(4;8),\)\(C(12;0).\)
a) Gọi F là chi phí luyện tập (đơn vị: nghìn đồng), ta có: \(F = 50y\)
Tính giá trị của F tại các đỉnh của tứ giác:
Tại \(O(0;0),\)\(F = 50.0 = 0\)
Tại \(A(0;10),\)\(F = 50.10 = 500\)
Tại \(B(4;8),\)\(F = 50.8 = 400\)
Tại \(C(12;0).\)\(F = 50.0 = 0\)
F đạt giá trị nhỏ nhất bằng 0 tại \(O(0;0),\)\(C(12;0).\)
Vậy bạn Mạnh cần đạp xe 12 giờ hoặc không tập thể dục..
b) Gọi T là lượng calo tiêu hao (đơn vị: calo), ta có: \(T = 350x + 700y\)
Tính giá trị của F tại các đỉnh của tứ giác:
Tại \(O(0;0),\)\(T = 350.0 + 700.0 = 0\)
Tại \(A(0;10),\)\(T = 350.0 + 700.10 = 7000\)
Tại \(B(4;8),\)\(T = 350.4 + 700.8 = 7000\)
Tại \(C(12;0),\)\(T = 350.12 + 700.0 = 4200\)
T đạt giá trị lớn nhất bằng 7000 tại \(A(0;10),\)\(B(4;8).\)
Vậy bạn Mạnh có thể chọn một trong hai phương án: Tập tạ 10 giờ hoặc đạp xe 4 tiếng và tập tạ 8 tiếng.

Để gắn nhãn cho các ghế ta chọn chọn 1 chữ cái in hoa và 1 số (từ 1 đến 20).
Số cách chọn chữ cái in hoa: 26 cách (tương ứng với 26 chữ)
Số cách chọn số: 20 cách
Vậy số ghế gắn nhãn tối đa là 26.20 = 520 (ghế)
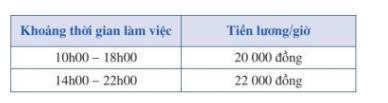



Có
Số tiền phạt cho mỗi cái chén bị bể là \(20.000\). Số tiền phạt cho mỗi cái ly bị bể là \(25.000\). Tổng số tiền phạt không được vượt quá \(200.000\). Cần tìm số trường hợp tối đa có thể xảy ra. Các bước giải Thiết lập phương trình bất đẳng thức: Gọi \(x\) là số chén bị bể và \(y\) là số ly bị bể. Tổng số tiền phạt được tính bằng \(20.000x+25.000y\). Theo yêu cầu, tổng số tiền phạt không quá \(200.000\), nên bất đẳng thức được thiết lập là \(20.000x+25.000y\le 200.000\). Rút gọn bất đẳng thức: Chia cả hai vế của bất đẳng thức cho \(5.000\), ta được \(4x+5y\le 40\). Tìm các cặp giá trị nguyên không âm của \((x,y)\): .f5cPye ul{font-size:var(--m3t7);line-height:var(--m3t8);margin:10px 0 20px 0;padding-inline-start:24px}.f5cPye .WaaZC:first-of-type ul:first-child{margin-top:0}.f5cPye ul.qh1nvc{font-size:var(--m3t7);line-height:var(--m3t8)} Vì \(x\) và \(y\) là số lượng chén và ly bị bể, nên \(x,y\) phải là các số nguyên không âm. Các trường hợp có thể xảy ra được liệt kê bằng cách thử các giá trị của \(y\) từ \(0\) đến giá trị lớn nhất có thể: Nếu \(y=0\), thì \(4x\le 40\Rightarrow x\le 10\). Có \(11\) trường hợp cho \(x\) (từ \(0\) đến \(10\)). Nếu \(y=1\), thì \(4x+5\le 40\Rightarrow 4x\le 35\Rightarrow x\le 8\). Có \(9\) trường hợp cho \(x\) (từ \(0\) đến \(8\)). Nếu \(y=2\), thì \(4x+10\le 40\Rightarrow 4x\le 30\Rightarrow x\le 7\). Có \(8\) trường hợp cho \(x\) (từ \(0\) đến \(7\)). Nếu \(y=3\), thì \(4x+15\le 40\Rightarrow 4x\le 25\Rightarrow x\le 6\). Có \(7\) trường hợp cho \(x\) (từ \(0\) đến \(6\)). Nếu \(y=4\), thì \(4x+20\le 40\Rightarrow 4x\le 20\Rightarrow x\le 5\). Có \(6\) trường hợp cho \(x\) (từ \(0\) đến \(5\)). Nếu \(y=5\), thì \(4x+25\le 40\Rightarrow 4x\le 15\Rightarrow x\le 3\). Có \(4\) trường hợp cho \(x\) (từ \(0\) đến \(3\)). Nếu \(y=6\), thì \(4x+30\le 40\Rightarrow 4x\le 10\Rightarrow x\le 2\). Có \(3\) trường hợp cho \(x\) (từ \(0\) đến \(2\)). Nếu \(y=7\), thì \(4x+35\le 40\Rightarrow 4x\le 5\Rightarrow x\le 1\). Có \(2\) trường hợp cho \(x\) (từ \(0\) đến \(1\)). Nếu \(y=8\), thì \(4x+40\le 40\Rightarrow 4x\le 0\Rightarrow x=0\). Có \(1\) trường hợp cho \(x\) (là \(0\)). Nếu \(y>8\), thì \(5y>40\), nên không có giá trị \(x\) nguyên không âm nào thỏa mãn. Tính tổng số trường hợp: Tổng số trường hợp là tổng của số trường hợp cho \(x\) ở mỗi giá trị của \(y\): \(11+9+8+7+6+4+3+2+1=51\). Kết quả cuối cùng Có tối đa \(51\) trường hợp xảy ra để chị Hoa bị phạt không quá \(200\text{\ nghìn}\)