K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 9 2016
\(A=\sqrt{x^2+2x+1}+\sqrt{x^2-2x+1}=\sqrt{\left(x+1\right)^2}+\sqrt{\left(x-1\right)^2}\)
\(=\left|x+1\right|+\left|x-1\right|=\left|x+1\right|+\left|1-x\right|\)
Áp dụng bđt \(\left|A\right|+\left|B\right|\ge\left|A+B\right|\) ta có:
\(A\ge\left|x+1+1-x\right|=2\)
Vậy GTNN của A là 2 khi \(-1\le x\le1\)
IM
11 tháng 9 2016
Ta có
\(A=\sqrt{x^2+2x+1}+\sqrt{x^2-2x+1}\)
\(\Rightarrow A=\sqrt{\left(x+1\right)^2}+\sqrt{\left(x-1\right)^2}\)
\(\Rightarrow A=\left|x+1\right|+\left|x-1\right|\)
\(\Rightarrow A=\left|x+1\right|+\left|1-x\right|\)
Vì \(\begin{cases}\left|x+1\right|\ge x+1\\\left|1-x\right|\ge1-x\end{cases}\)\(\Rightarrow\left|x+1\right|+\left|1-x\right|\ge x+1+1-x\)
\(\Rightarrow\left|x+1\right|+\left|1-x\right|\ge2\)
Dấu " = " xảy ra khi \(\begin{cases}x+1\ge0\\1-x\ge0\end{cases}\)\(\Leftrightarrow\begin{cases}x\ge-1\\x\le1\end{cases}\)
Vậy MINA=2 khi \(-1\le x\le1\)
TK
13 tháng 9 2017
\(\frac{-3}{\sqrt{x}+1}=\frac{-3}{\sqrt{4}+1}=\frac{-3}{2+1}=\frac{-3}{3}=-1\)
2 tháng 1 2016
\(A=5x+\frac{180}{x-1}=5\left(x-1\right)+\frac{180}{x-1}+5\ge2\sqrt{5\left(x-1\right).\frac{180}{x-1}}+5\)
VT
3
10 tháng 10 2021
\(M=\frac{\sqrt{x}}{\sqrt{x}+1}\left(x\ge0\right)\)
Khi \(M=\sqrt{x}-2\)
\(\Rightarrow\frac{\sqrt{x}}{\sqrt{x}+1}=\sqrt{x}-2\)
\(\Leftrightarrow\sqrt{x}=\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)\)
\(\Leftrightarrow\sqrt{x}=x+\sqrt{x}-2\sqrt{x}-2\)
\(\Leftrightarrow\sqrt{x}=x-\sqrt{x}-2\)
\(\Leftrightarrow x-\sqrt{x}-\sqrt{x}-2=0\)
\(\Leftrightarrow x-2\sqrt{x}+1-3=0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2=3\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2=\left(\pm\sqrt{3}\right)^2\)
\(\Leftrightarrow\sqrt{x}-1=\pm\sqrt{3}\)
\(\Leftrightarrow\sqrt{x}=\pm\sqrt{3}+1\)
\(\Leftrightarrow\orbr{\begin{cases}x=\left(\sqrt{3}+1\right)^2\\x=\left(-\sqrt{3}+1\right)^2\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=3+2\sqrt{3}+1\\1-2\sqrt{3}+3\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=4+2\sqrt{3}\\x=4-2\sqrt{3}\end{cases}}\)
Vậy \(x\in\left\{4\pm2\sqrt{3}\right\}\)khi \(M=\sqrt{x}-2\)
31 tháng 7 2016
\(A=\sqrt{x^2+2x+1}+\sqrt{x^2-2x+1}\)
\(=\sqrt{\left(x+1\right)^2}+\sqrt{\left(x-1\right)^2}\)
-Nêú \(x\ge1\)thì \(\sqrt{\left(x+1\right)^2}=x+1\)và\(\sqrt{\left(x-1\right)^2}=x-1\)
Ta có:\(A=x+1+x-1=2x\ge2\)
Dấu "=" xảy ra khi x=1
-Nếu\(1>x\ge-1\)thì \(\sqrt{\left(x+1\right)^2}=x+1\)và\(\sqrt{\left(x-1\right)^2}=1-x\)
Ta có:\(A=x+1+1-x=2\)
-Nếu x<-1 thì \(\sqrt{\left(x+1\right)^2}=-x-1\)và\(\sqrt{\left(x-1\right)^2}=1-x\)
Ta có:\(A=-x-1+1-x=-2x\ge2\)
Dấu "=" xảy ra khi x=-1
Vậy GTNN của A là 2 tại x=1 hoặc x=-1
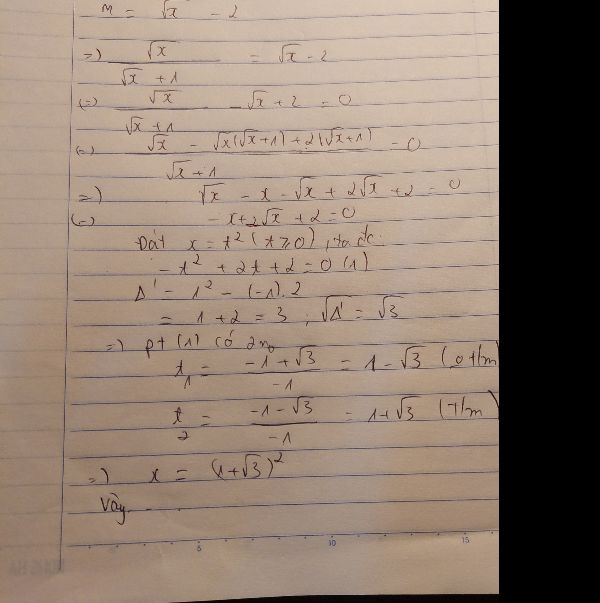
Còn phải hỏi bằng 2 ❗❗❗
2:))