Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

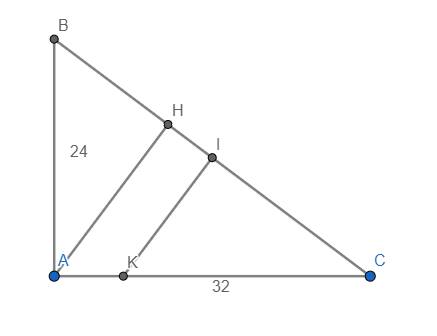
Ta có \(\widehat{HAC}=\widehat{B}\) (cùng phụ với \(\widehat{C}\))
Mà \(\widehat{B}=\tan^{-1}\left(\dfrac{AC}{AB}\right)=\tan^{-1}\left(\dfrac{32}{24}\right)=\tan^{-1}\left(\dfrac{4}{3}\right)\approx53,13^o\)
Nên \(\widehat{HAC}\approx53,13^o\)
Ta có \(BC=\sqrt{AB^2+AC^2}=\sqrt{24^2+32^2}=40\) cm
\(\Rightarrow IB=IC=20cm\)
Ta có \(CH=\dfrac{AC^2}{BC}=\dfrac{32^2}{40}=25,6cm\)
\(AH=\dfrac{AB.AC}{BC}=\dfrac{24.32}{40}=19,2cm\)
Do vậy \(\dfrac{CI}{CH}=\dfrac{IK}{AH}\Rightarrow IK=\dfrac{CI.AH}{CH}=\dfrac{20.19,2}{25,6}=15cm\)
Mặt khác \(\dfrac{CI}{CH}=\dfrac{CK}{CA}\Rightarrow CK=\dfrac{CI.CA}{CH}=\dfrac{20.32}{25,6}=25cm\)
\(\Rightarrow C_{CIK}=CI+CK+IK\) \(=20+15+25=60cm\)
Mặt khác, \(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}.24.32=384cm^2\)
Lại có \(\Delta CIK~\Delta CAB\left(g.g\right)\) \(\Rightarrow\dfrac{S_{CIK}}{S_{CAB}}=\left(\dfrac{IK}{AB}\right)^2=\left(\dfrac{15}{24}\right)^2=\dfrac{25}{64}\)
\(\Rightarrow S_{CIK}=\dfrac{25}{64}S_{CAB}=\dfrac{25}{64}.384=150cm^2\)

a, \(\Delta ABC,\hat{BAC}=90^o\)
\(\Rightarrow BC^2=AB^2+AC^2\)(định lý Py-ta-go)
\(\Leftrightarrow10^2=6^2+AC^2\)
\(\Leftrightarrow AC^2=64\)
\(\Leftrightarrow AC=8\left(cm\right)\)
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông vào \(\Delta ABC, \hat{BAC}=90^o, AH\perp BC\) ta có:
\(AB^2=BH.BC\Leftrightarrow6^2=BH.10\Leftrightarrow BH=3,6\left(cm\right)\)
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{AH^2}=\frac{1}{6^2}+\frac{1}{8^2}\Leftrightarrow\frac{1}{AH^2}=\frac{25}{576}\)\(\Leftrightarrow AH^2=\frac{576}{25}\Leftrightarrow AH=4,8\left(cm\right)\)
Chu vi tam giác ABC: 6 + 10 + 8 = 24 (cm)
Diện tích tam giác ABC: \(\frac{4,8.10}{2}=24\left(cm^2\right)\)

A B C 6 10 H D M N
a, Xét tam giác ABC vuông tại A, đường cao AH
Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(AB^2+AC^2=BC^2\Rightarrow AC^2=BC^2-AC^2=100-36=64\Leftrightarrow AC=8\)cm
* Áp dụng hệ thức :
\(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{36}{10}=\frac{18}{5}\)cm
* Áp dụng hệ thức :
\(AH^2=CH.BH\)mà \(BC-BH=CH\Rightarrow CH=10-\frac{18}{5}=\frac{32}{5}\)cm
\(\Rightarrow AH^2=\frac{32}{5}.\frac{18}{5}=\frac{576}{25}\Rightarrow AH=\frac{24}{5}\)cm
Chu vi tam giác ABC là : \(P_{ABC}=AB+AC+BC=6+10+8=24\)cm
Diện tích tam giác ABC là : \(S_{ABC}=\frac{1}{2}AB.AC=\frac{1}{2}.6.8=24\)cm2
b, Ta có AD là phân giác nên : \(\frac{AB}{BC}=\frac{BD}{CD}\)( t/c )
\(\Rightarrow\frac{CD}{BC}=\frac{BD}{AB}\)( tỉ lệ thức )
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{CD}{BC}=\frac{BD}{AB}=\frac{CD+BD}{AB+BC}=\frac{BC}{16}=\frac{1}{2}\)
\(\Rightarrow\frac{BD}{6}=\frac{1}{2}\Rightarrow BD=3\)cm
\(\Rightarrow HD=BH-BD=\frac{18}{5}-3=\frac{3}{5}\)cm
Áp dụng định lí Pytago cho tam giác ADH vuông tại H ta có :
\(AD^2=HD^2+AH^2=\frac{9}{25}+\frac{576}{25}=\frac{585}{25}\Rightarrow AD=\frac{3\sqrt{65}}{5}\)cm
Sửa đề: Chứng minh \(\frac{S_{ABI}}{S_{AMN}}=\frac{1}{2\cdot\sin^2B}+\frac{1}{2cos^2HAC}\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC;AB^2=BH\cdot BC;AC^2=CH\cdot CB\)
Ta có: \(\frac{1}{2\cdot\sin^2B}+\frac{1}{2cos^2HAC}\)
\(=\frac{1}{2\cdot\sin^2B}+\frac{1}{2\cdot cos^2B}=\frac12\left(\frac{1}{\sin^2B}+\frac{1}{cos^2B}\right)\)
\(=\frac12\cdot\frac{\sin^2B+cos^2B}{\left(\sin B\cdot cosB\right)^2}=\frac12\cdot\frac{1}{\left(\sin B\cdot cosB\right)^2}\)
\(=\frac12\cdot\frac{1}{\left(\frac{AC}{BC}\cdot\frac{AB}{BC}\right)^2}=\frac12\cdot\frac{1}{\left(\frac{AB\cdot AC}{BC^2}\right)^2}=\frac12\cdot\left(\frac{1}{\frac{AH\cdot BC}{BC^2}}\right)^2\)
\(=\frac12\cdot\left(\frac{BC}{AH}\right)^2\) (2)
Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\)
=>\(AM=\frac{AH^2}{AB}\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AH^2=AN\cdot AC\)
=>\(AN=\frac{AH^2}{AC}\)
ΔABC có AH là đường cao
nên \(S_{ABC}=\frac12\cdot AH\cdot BC\)
ΔAMN vuông tại A
=>\(S_{AMN}=\frac12\cdot AM\cdot AN=\frac12\cdot\frac{AH^2}{AB}\cdot\frac{AH^2}{AC}=\frac12\cdot\frac{AH^4}{AH\cdot BC}=\frac12\cdot\frac{AH^3}{BC}\)
=>\(\frac{S_{AMN}}{S_{ABC}}=\frac{AH^3}{2\cdot BC}:\frac{AH\cdot BC}{2}=\frac{AH^3}{2\cdot BC}\cdot\frac{2}{AH\cdot BC}=\frac{AH^2}{BC^2}\)
=>\(\frac{S_{ABC}}{S_{AMN}}=\frac{BC^2}{AH^2}\)
I là trung điểm của BC
=>\(\frac{BI}{BC}=\frac12\)
=>\(S_{ABC}=2\cdot S_{ABI}\)
Ta có: \(\frac{S_{ABC}}{S_{AMN}}=\frac{BC^2}{AH^2}\)
=>\(\frac{2\cdot S_{ABI}}{S_{AMN}}=\frac{BC^2}{AH^2}\)
=>\(\frac{S_{ABI}}{S_{AMN}}=\frac{BC^2}{2AH^2}=\frac12\cdot\left(\frac{BC}{AH}\right)^2\) (1)
Từ (1),(2) suy ra \(\frac{S_{ABI}}{S_{AMN}}=\frac{1}{2\cdot\sin^2B}+\frac{1}{2cos^2HAC}\)