PT
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 8
a: (x-2)(x+3)>0
TH1: \(\begin{cases}x-2>0\\ x+3>0\end{cases}\Rightarrow\begin{cases}x>2\\ x>-3\end{cases}\Rightarrow x>2\)
TH2: \(\begin{cases}x-2<0\\ x+3<0\end{cases}\Rightarrow\begin{cases}x<2\\ x<-3\end{cases}\)
=>x<-3
b: (2x-1)(-x+1)>0
=>(2x-1)(x-1)<0
TH1: \(\begin{cases}2x-1>0\\ x-1<0\end{cases}\Longrightarrow\begin{cases}x>\frac12\\ x<1\end{cases}\)
=>\(\frac12
TH2: \(\begin{cases}2x-1<0\\ x-1>0\end{cases}\Rightarrow\begin{cases}x<\frac12\\ x>1\end{cases}\)
=>x∈∅
c: (x+1)(3x-6)<0
=>3(x+1)(x-2)<0
=>(x+1)(x-2)<0
TH1: \(\begin{cases}x+1>0\\ x-2<0\end{cases}\Rightarrow\begin{cases}x>-1\\ x<2\end{cases}\Rightarrow-1
TH2: \(\begin{cases}x+1<0\\ x-2>0\end{cases}\Rightarrow\begin{cases}x<-1\\ x>2\end{cases}\)
=>x∈∅
NQ
Nguyễn Quốc Đạt
CTVVIP
13 tháng 9
Admin thật thường có nhãn Admin kèm theo sau tên bạn nhé, bạn lưu ý để tránh kẻ xấu lợi dụng.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 9
Cô chào em, những người làm việc cho Olm thì đều phải có gắn chức danh kèm theo, em nhé. Nếu tên hiển thị mà không kèm theo chức danh thì tất cả những tài khoản đó đều giả mạo.
24 tháng 2 2019
a) 1cm + 2cm = 3cm < 4cm
⇒ bộ ba đoạn thẳng 1cm, 2cm, 4cm không thể tạo thành 1 tam giác.
b) 2cm + 3cm = 5cm.
⇒ Bộ ba đoạn thẳng 2cm; 3cm; 5cm không lập thành tam giác.
c) Ta có 3cm + 4cm = 7cm > 5cm.
Do đó bộ đoạn thẳng 3cm, 4cm, 5cm có thể thành 3 cạnh của tam giác.
Cách dựng tam giác có ba độ dài 3cm, 4cm, 5cm :
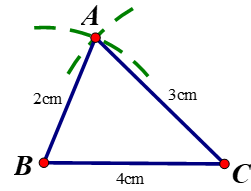
- Vẽ BC = 4cm
- Dựng đường tròn tâm B bán kính 2cm ; đường tròn tâm C bán kính 3cm. Hai đường tròn cắt nhau tại A. Nối AB, AC ta được tam giác cần dựng.
CT
0
6 tháng 3 2019
Giải :
Hình vẽ ; giả thiết, kết luận đã được đầu bài cho sẵn.
Chứng minh :
Xét \(\Delta AMC\text{ và }\Delta BMD\), có :
\(MA=MB\text{ (gt)}\)
\(\angle AMC=\angle DMB\text{ (đối đỉnh)}\)
\(DM=CM\text{ (gt)}\)
\(\Rightarrow\Delta AMC=\Delta BMD\text{ (c.g.c)}\)
10 tháng 3 2019
b/ Ta có : \(\bigtriangleup AMC=\bigtriangleup BMD\text{ (c.m.t)}\)
\(\Rightarrow\widehat{DBM}=\widehat{ACM}\text{ (2 góc tương ứng ở vị trí so le trong)}\) (1)
\(\Rightarrow BD//AC\)
Xét \(\bigtriangleup DMA\text{ và }\bigtriangleup BMC,\text{ có :}\)
\(\widehat{DMA}=\widehat{BMC}\text{ (đối đỉnh)}\)
\(DM=CM\left(gt\right)\)
\(BM=AM\left(gt\right)\)
\(\Rightarrow\bigtriangleup DMA=\bigtriangleup BMC\left(c.g.c\right)\)
\(\Rightarrow\widehat{ADM}=\widehat{DCM}\text{ (2 góc tương ứng ở vị trí so le trong)}\) (2)
\(\text{Từ (1) và (2) suy ra tứ giác ABCD là hình bình hành}\) (3)
\(\angle ACB=90^{\text{o}}\) (4)
\(\text{T}ừ\text{ (3) và (4) suy ra hình bình hành ABCD là hình chữ nhật}\) (đpcm)
1 tháng 10 2016
Bài 1: Tính B = 1 + 2 + 3 + ... + 98 + 99
Số số hạng của B là : 99 số hạng
Tổng của B là ( 1 + 99 ) x 99 : 2 = 4950
Vậy : B = 1 + 2 + 3 + ... + 98 + 99 = 4950
Bài 2: Tính C = 1 + 3 + 5 + ... + 997 + 999
Số số hạng của C là : ( 999 - 1 ) : 2 + 1 = 500 ( số hạng )
Tổng của C là : ( 1 + 999 ) x 500 : 2 = 250000
Bài 3. Tính D = 10 + 12 + 14 + ... + 994 + 996 + 998
Số số hạng của D là : ( 998 - 10 ) : 2 + 1 = 495 ( số hạng )
Tổng của D là : ( 10 + 998 ) x 495 : 2 = 249480
TM
1 tháng 10 2016
!)
B=1+2+3+...+98+99
B= 99(99+1):2
B = 4950
( Áp dụng: Nếu B=1+2+3+...+(n-1)+n
thì B=n(n+1):2
B=4950 nha bạn!
2) Tính: C=1+3+5+...+997+999
Ta có: 999= 2(500)-1. n=500
1+2+3+...+(2n-1)= n^2
= 500^2= 250.000
C=25.000
\(2y^2+7y+11-\left(8y^2-5y+7\right)\)
\(=2y^2+7y+11-8y^2+5y-7\)
\(=-6y^2+12y+4\)
Bước 1: Phân phối dấu trừ vào biểu thức trong dấu ngoặc
\(2 y^{2} + 7 y + 11 - 8 y^{2} + 5 y - 7\)
Bước 2: Gom các hạng tử giống nhau
Kết quả cuối cùng:
\(- 6 y^{2} + 12 y + 4\)
Vậy biểu thức rút gọn sẽ là:
\(- 6 y^{2} + 12 y + 4\)
Nếu bạn có bất kỳ câu hỏi nào thêm hoặc cần giải thích rõ hơn, đừng ngần ngại yêu cầu nhé!