Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!

A, B, C có bội số chung nhỏ nhất là 6

Các bước giải:

A= 1, B= 2, B=3

x= 8, y=5, z=3

Ax + By = Cz = 1 x 8 + 2 x 5 = 3 x 6

A, B, C có bội số chung nhỏ nhất là 6.

Chúc bạn học tốt!

Ta có \(\sqrt{2+2\cos2x}=\sqrt{2+2\left(2\cos^2x-1\right)}=\sqrt{4\cos^2x}=2\left|\cos x\right|\)

\(\Leftrightarrow f\left(x\right)+f\left(-x\right)=2\left|\cos x\right|,\forall x\inℝ\)  (1)

Đặt \(g\left(x\right)=f\left(x\right)-\left|\cos x\right|\)

Khi đó (1) \(\Leftrightarrow\left[f\left(x\right)-\left|\cos x\right|\right]+\left[f\left(-x\right)-\left|\cos x\right|\right]=0\)

\(\Leftrightarrow g\left(x\right)+\left[f\left(-x\right)-\left|\cos\left(-x\right)\right|\right]=0\) (do \(\cos x\) là hàm chẵn)

\(\Leftrightarrow g\left(x\right)+g\left(-x\right)=0\)

\(\Leftrightarrow g\left(x\right)=-g\left(-x\right)\)

\(\Leftrightarrow g\left(x\right)\) là hàm lẻ

Khi đó \(f\left(x\right)=g\left(x\right)+\left|\cos x\right|\) với \(g\left(x\right)\) là hàm lẻ. Thử lại, ta thấy:

(1) \(\Leftrightarrow f\left(x\right)+f\left(-x\right)=g\left(x\right)+\left|\cos x\right|+g\left(-x\right)+\left|\cos\left(-x\right)\right|\)

\(\Leftrightarrow f\left(x\right)+f\left(-x\right)=2\left|\cos x\right|\), thỏa mãn

 Vậy \(f\left(x\right)=g\left(x\right)+\left|\cos x\right|\) với \(g\left(x\right)\) là hàm lẻ bất kì có tập xác định là \(ℝ\)

 \(\Rightarrow I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}f\left(x\right)dx\)

 \(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left[g\left(x\right)+\left|\cos x\right|\right]dx\)

\(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}g\left(x\right)dx+\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left|\cos x\right|dx\)

\(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left|\cos x\right|dx\) (do \(g\left(x\right)\) là hàm lẻ)

\(I=\int\limits^{-\dfrac{\pi}{2}}_{-\dfrac{3\pi}{2}}\left(-\cos x\right)dx+\int\limits^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}\cos xdx+\int\limits^{\dfrac{3\pi}{2}}_{\dfrac{\pi}{2}}\left(-\cos x\right)dx\)

\(I=-\sin x|^{-\dfrac{\pi}{2}}_{-\dfrac{3\pi}{2}}+\sin x|^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}-\sin x|^{\dfrac{3\pi}{2}}_{\dfrac{\pi}{2}}\)

\(I=6\)

  \(x=3y\) và y = 5\(x\)  thay y = 5\(x\) vào \(x\) = 3y ta có: \(x\) = 3.5\(x\) 

    ⇒ \(x\)   = 15\(x\) ⇒ \(x-15x\) = 0 ⇒ \(-14\)\(x\) = 0 ⇒ \(x=0\)

Thay \(x\) = 0 vào y = 5\(x\) ta được:  y= 5.0 = 0

Vậy \(x=3\)y; y = 5\(x\) thì y = 0 

\(y=\dfrac{x^2-\left(x^2+4mx+1\right)}{x+\sqrt{x^2+4mx+1}}=\dfrac{-4mx-1}{x+\sqrt{x^2+4mx+1}}\)

\(=\dfrac{-4mx-1}{x+\left|x\right|\sqrt{1+\dfrac{4m}{x}+\dfrac{1}{x^2}}}\)

\(\lim\limits_{x\rightarrow\pm\infty}y\dfrac{-4m-\dfrac{1}{x}}{1\pm\sqrt{1+\dfrac{4m}{x}+\dfrac{1}{x^2}}}=-4m\)

Để y = 1 là TCN => -4m = 1 => m = -1/4 

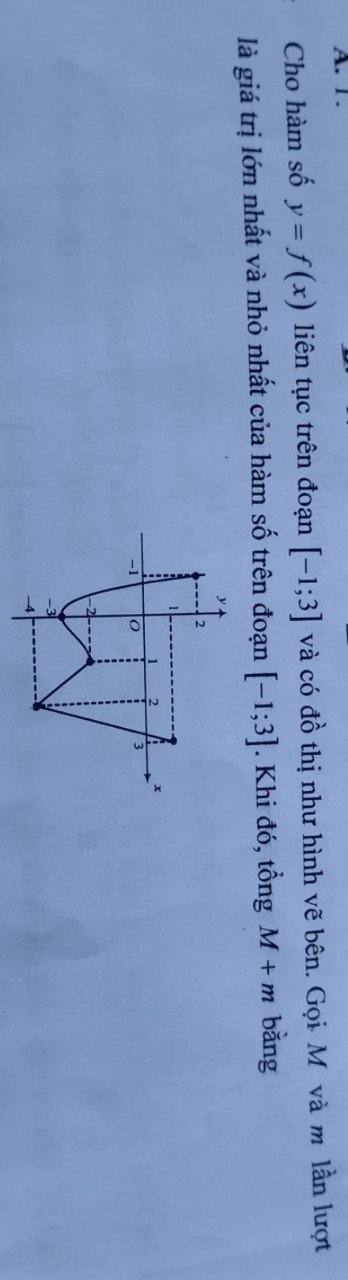
Dựa vào đồ thị, ta thấy \(m=\min\limits_{\left[-1;3\right]}f\left(x\right)=f\left(2\right)=-4\)

và \(M=\max\limits_{\left[-1;3\right]}f\left(x\right)=f\left(-1\right)=2\)

Khi đó \(M+m=2-4=-2\)

a, A''Có đúng 2 nữ''

\(C^2_3.C_{56}^2\)

\(P\left(A\right)=\dfrac{C_3^2.C_{56}^2}{C_{59}^4}\)

b, B''Có ít nhất 2 nam''

TH1 : Có 2 nam \(C_{56}^2.C_3^2\)

TH2 : Có 3 nam \(C_{56}^3.C_3^1\)

TH3 : Có 4 nam \(C^4_{56}\)

\(\Rightarrow C_{56}^2.C_3^2+C_{56}^3.C_3^1+C_{56}^4\)

\(P\left(B\right)=\dfrac{C_{56}^2.C_3^2+C_{56}^3.C_3^1+C_{56}^4}{C_{59}^4}\)

c, C''Có nhiều nhất 2 nam''

TH1 : Có 1 nam \(C_{56}^1.C_3^3\)

TH2 : Có 2 nam \(C_{56}^2.C_3^2\)

\(\Rightarrow C_{56}^2.C_3^3+C_{56}^2.C_3^2\)

\(P\left(C\right)=\dfrac{C_{56}^2.C_3^3+C^2_{56}.C_3^2}{C_{59}^4}\)