Chứng minh rằng với mọi a,b,c dương ta luôn có
1/(a(1+b))+1/(b(1+c))+1/(c(1+a))≤3/(1+abc)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho a,b,c là các số thực dương thỏa mãn a+b+c = 3
Chứng minh rằng với mọi k > 0 ta luôn có....
.
Cho a,b,c là các số thực dương thỏa mãn a+b+c = 3
Chứng minh rằng với mọi k > 0 ta luôn có

Ta có: a/(a+b) > a/(a+b+c)
b/(b+c) > b/(b+c+a)
c/(c+a) > c/(c+a+b)
=> [a/(a+b)] + [b/(b+c)] + [c/(c+a)] > [a/(a+b+c)] + [b/(a+b+c)] + [c/(a+b+c)]
=> [a/(a+b)] + [b/(b+c)] + [c/(c+a)] > 1
Lại có: a/(a+b) < (a+b)/(a+b+c)
b/(b+c) < (b+c)/(b+c+a)
c/(c+a) < (c+a)/(c+a+b)
=> [a/(a+b)] + [b/(b+c)] + [c/(c+a)] < [(a+b)/(a+b+c)] + [(b+c)/(a+b+c)] + [(c+a)/(a+b+c)]
=> [a/(a+b)] + [b/(b+c)] + [c/(c+a)] < [2.(a+b+c)]/(a+b+c)
=> [a/(a+b)] + [b/(b+c)] + [c/(c+a)] < 2
Vậy .....

Điều kiện x ≠ 1 và x ≠ - 1
Ta có:

Biểu thức dương khi x 2 + 2 x + 3 > 0
Ta có: x 2 + 2 x + 3 = x 2 + 2 x + 1 + 2 = x + 1 2 + 2 > 0 với mọi giá trị của x.
Vậy giá trị của biểu thức dương với mọi giá trị x ≠ 1 và x ≠ - 1

Điều kiện x ≠ 0 và x ≠ -3
Ta có:
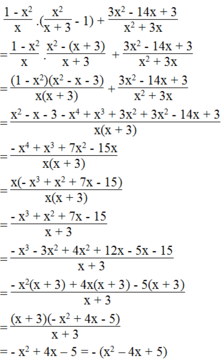
Vì x 2 - 4 x + 5 = x 2 - 4 x + 4 + 1 = x - 2 2 + 1 > 0 với mọi giá trị của x nên
- x 2 + 4 x - 5 = - x - 2 2 + 1 < 0 với mọi giá trị của x.
Vậy giá trị biểu thức luôn luôn âm với mọi giá trị x ≠ 0 và x ≠ -3

cái nàyt nghĩ chỉ có cách quy đồng rồi chứng minh BĐT luôn đúng thôi bạn!
^_^