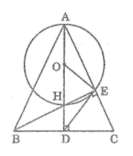
Cho tam giác ABC cân tại A, các đường cao AD và BE cắt nhau tại H. Vẽ đường tròn (O) có đường kính AH. Cm:
a) Điểm E nằm trên đường tròn (O).
b) DE là tiếp tuyến của (O)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 9 2017
Ta có : OH = OE
Suy ra tam giác OHE cân tại O
Trong tam giác BDH ta có:
Từ (1), (2) và (3) suy ra:
Tam giác ABC cân tại A có AD ⊥ BC nên BD = CD
Tam giác BCE vuông tại E có ED là đường trung tuyến nên:
ED = DB = BC/2 (tính chất tam giác vuông)
Suy ra tam giác BDE cân tại D
Suy ra: DE ⊥ EO. Vậy DE là tiếp tuyến của đường tròn (O).
CM
30 tháng 10 2017
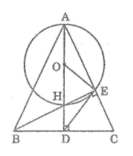
Gọi O là trung điểm của AH
Tam giác AEH vuông tại E có EO là đường trung tuyến nên :
EO = OA = OH = AH/2 (tính chất tam giác vuông)
Vậy điểm E nằm trên đường tròn (O ; AH/2 )
3 tháng 8 2018
a/ Xét \(\Delta AEH\)vuông tại E có:
EO là đường trung tuyến ( OA=OH )
\(\Rightarrow EO=\frac{1}{2}AH=OA=OH\)( tính chất đường trung tuyến trong tam giác vuông )
\(\Rightarrow E\)nằm trên đường tròn tâm O đường kính AH
b/ Xét \(\Delta OHE\)có:
OH=OE ( cmt )
\(\Rightarrow\Delta OHE\)cân tại O
\(\Rightarrow\widehat{OEH}=\widehat{OHE}\)( tính chất tam giác cân )
Mà: \(\widehat{BHD}=\widehat{OHE}\)( 2 góc đối đỉnh )
\(\Rightarrow\widehat{OEH}=\widehat{BHD}\left(=\widehat{OHE}\right)\)(1)
Xét \(\Delta ABC\)cân tại A có:
AD là đường cao ( gt )
\(\Rightarrow AD\)là đường trung tuyến
\(\Rightarrow BD=CD\)
Xét \(\Delta BEC\)vuông tại E có:
ED là đường trung tuyến ( BD=CD )
\(\Rightarrow ED=\frac{1}{2}BC=BD\)( tính chất đường trung tuyến trong tam giác vuông )
\(\Rightarrow\Delta BDE\)cân tại D
\(\Rightarrow\widehat{DEH}=\widehat{DBH}\)(2)
Từ (1) và (2) suy ra: \(\widehat{OEH}+\widehat{DEH}=\widehat{BHD}+\widehat{DBH}\)
Hay \(\widehat{OED}=90\)( \(\widehat{BHD}\)và \(\widehat{DBH}\)là 2 góc phụ nhau của \(\Delta BHD\)vuông tại D )
\(\Rightarrow DE\perp OE\)
Vậy DE là tiếp tuyến của đường tròn (O).
HH
16 tháng 7 2020
Tớ chỉ làm được mỗi câu a,b thôi nên bạn thông cảm =))
a) Vì OE = OA = OH nên':
=> E nằm trên đường tròn (O) có đường kính AH
b) Xét tam giác vuông BEC
Có : ED là đường trung tuyến ứng với cạnh huyền
=> ED = DB
=> \(\widehat{E_1}=\widehat{B_1}\left(1\right)\)
Ta lại có : \(\widehat{E_2}=\widehat{H_1}=\widehat{H_2}\left(2\right)\)
Từ (1)(2) , suy ra :
\(\widehat{E_1}+\widehat{E_2}=\widehat{B_1}+\widehat{H_2}=90^o\)
Vậy : DE vuông góc với bán kính OE tại E nên DE là tiếp tuyến của đường tròn (O)