Cho tam giác ABC vuông tại A , đường phân giác BE , Kẻ EH vuông góc với BC ( H thuộc BC ) , gọi K là giao điểm của AB và HE , chứng minh rằng :
a , Tam giác ABE = tam giác HBE
b , BE lvuông góc AH
c , EK = EC
d , AE < EC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 3 2022
tham khảo
a) Xét tam giác vuông ABE và tam giác vuông HBE (^BAE = ^BHE = 90o)
BE chung
^ABE = ^HBE (BE là phân giác ^ABC)
=> tam giác vuông ABE = tam giác vuông HBE (ch - gn)
b) Ta có: AE = HE (tam giác vuông ABE = tam giác vuông HBE)
=> E thuộc đường trung trực của AH (1)
Ta có: AB = HB (tam giác vuông ABE = tam giác vuông HBE)
=> B thuộc đường trung trực của AH (2)
Từ (1) và (2) => BE là đường trung trực của AH (đpcm)
c) Ta có: ^BEK = ^BEA + ^AEK
^BEC = ^BEH + ^HEC
Mà ^BEA = ^BEH (tam giác vuông ABE = tam giác vuông HBE)
^AEK = ^HEC (2 góc đối đỉnh)
=> ^BEK = ^BEC
Xét tam giác BEK và tam giác BEC:
^BEK = ^BEC (cmt)
^KBE = ^CBE (BE là phân giác ^ABC)
BE chung
=> tam giác BEK = tam giác BEC (g - c - g)
=> EK = EC (cặp cạnh tương ứng)
28 tháng 10 2023
1. ΔABE = ΔHBE
Xét ΔABE và ΔHBE, ta có :
BE là cạnh chung.
=> ΔABE = ΔHBE
2. BE là đường trung trực của AH :
BA =BH và EA = EH (ΔABE = ΔHBE)
=> BE là đường trung trực của AH .
3. EK = EC
Xét ΔKAE và ΔCHE, ta có :
EA = EH (cmt)
=> ΔKAE và ΔCHE
=> EK = EC
4. EC > AC
Xét ΔKAE vuông tại A, ta có :
KE > AE (KE là cạnh huyền)
Mà : EK = EC (cmt)
=> EC > AC.
29 tháng 7 2016
1. ΔABE = ΔHBE
Xét ΔABE và ΔHBE, ta có :
BE là cạnh chung.
=> ΔABE = ΔHBE
2. BE là đường trung trực của AH :
BA =BH và EA = EH (ΔABE = ΔHBE)
=> BE là đường trung trực của AH .
3. EK = EC
Xét ΔKAE và ΔCHE, ta có :
EA = EH (cmt)
=> ΔKAE và ΔCHE
=> EK = EC
4. EC > AC
Xét ΔKAE vuông tại A, ta có :
KE > AE (KE là cạnh huyền)
Mà : EK = EC (cmt)
=> EC > AC.
TN
20 tháng 8 2015
a) xet tam giac ABE vuong tai A va tam giac HBE vuong tai H ta co
BE=BE ( canh chung) ; goc ABE= goc HBE ( BE la tia p/g goc B)
--> tam giac ABE= tam giac HBE ( ch=gn)
b) ta co
BA=BH ( tam giac ABE= tam giac HBE)
EA=EH( tam giac ABE= tam giac HBE)
==> BE la duong trung truc cua AH
c) xet tam giac EKA va tam giac ECH ta co
AE=EH ( tam giacABE= tam giacHBE) ; goc EAK= goc EHC (=90); goc AEK= goc HEC ( 2 goc doi dinh )
--> tam giac EKA = tam giac ECH ( g--c-g)
--> EK=EC (2 canh tuong ung )
d) tu diem E den duong thang HC ta co :
EH la duong vuong goc ( EH vuong goc BC)
EC la duong xien
-> EH<EC ( quan he duong xien duong vuong goc)
ma EH= AE ( tam giac ABE= tam giac HBE)
nen AE < EC
3 tháng 5 2017
Cho tam giác ABC vuông tại a ; đường phân giác BE. kẻ EH cuông góc BC(H thuộc BC) Gọi K là giao điểm của AB và HE . Chứng minh rằng
1) Tam giác ABE=tam giác HBE
2) BE là đường trung trực của đoạn thẳng AH; Chứng minh BE vuông góc KC
3) AE<EC
28 tháng 7 2023
a: Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔABE=ΔHBE
b: ΔBAE=ΔBHE
=>BA=BH và EA=EH
=>BE là trung trực của AH
c: Xét ΔEAK vuông tại A và ΔEHC vuông tại H có
EA=EH
góc AEK=góc HEC
=>ΔEAK=ΔEHC
=>EK=EC
=>ΔEKC cân tại E
DN
7 tháng 3 2022
a, xét tam giác ABE và tam giác HBE có : BE chung
góc BAE = góc BHE = 90 do ...
góc ABE = góc HBE do BE là phân giác ...
=> tam giác ABE = tam giác HBE (ch - gn)
=> AE = EH
b, xét 2 tam giác vuông EAK và EHC có:
EA=EH(theo câu a)
ˆAEKAEK^=ˆHECHEC^(vì đối đỉnh)
=> t.giác EAK=t.giác EHC(cạnh góc vuông-góc nhọn)
=> EK=EC(2 cạnh tương ứng)
c, ta thấy E là trực tâm của tam giác CKB
=> BE⊥⊥CK
7 tháng 3 2022
tham khảo
a, xét tam giác ABE và tam giác HBE có : BE chung
góc BAE = góc BHE = 90 do ...
góc ABE = góc HBE do BE là phân giác ...
=> tam giác ABE = tam giác HBE (ch - gn)
=> AE = EH
b, xét 2 tam giác vuông EAK và EHC có:
EA=EH(theo câu a)
ˆAEKAEK^=ˆHECHEC^(vì đối đỉnh)
=> t.giác EAK=t.giác EHC(cạnh góc vuông-góc nhọn)
=> EK=EC(2 cạnh tương ứng)
c, ta thấy E là trực tâm của tam giác CKB
=> BE⊥CK
17 tháng 6 2023
a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔBAE=ΔBHE
=>EA=EH
b: Xét ΔEAK vuông tại A và ΔEHC vuông tại H có
EA=EH
góc AEK=góc HEC
=>ΔEAK=ΔEHC
=>EK=EC
c: BK=BC
EK=EC
=>BE là trung trực của CK
=>BE vuông góc CK
CM
10 tháng 11 2017
Xét ΔAEK vuông tại A và ΔHEC vuông tại H có:
AE = EH (chứng minh trên)
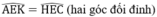
⇒ ΔAEK = ΔHEC (cạnh góc vuông – góc nhọn kề)
⇒ EK = EC (hai cạnh tương ứng)
khó thể xem trên mạng
Hình tự vẽ
a)Xét hai tam giác vuông ABE và HBE CÓ:
AE-chung
góc ABE=góc HBE(gt)
=>tam giác ABE=tam giác HBE(ch-gn)
b)Có tam giác ABE=tam giác HBE(cmt)
=>AB=BH
=>Tam giác BHA cân tại B
mà BE là p/g của góc ABH
=>BE là đường cao, đường trung tuyến
=>BE\(\perp\) AH
c)Xét tam giác AEK và tam giác HEC CÓ
góc KAE=góc EHC=900
AE=EH
góc AEK=góc HEC
=>tam giác AEK= tam giác HEC(c.g.c)
=>EK=EC
d)Xét tam giác EHC có góc EHC=900
=> EC là cạnh lớn nhất
=>EC>EH
Mà EH=AE
=>EC>AE