\(\text{Chứng minh trong một tam giác nhọn thì trọng tâm; trực tâm; tâm đường tròn ngoại tiếp thẳng hằng}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
Cắt mảnh bìa hình tam giác. Kẻ 2 đường trung tuyến của tam giác ABC, chúng cắt nhau tại G.
Đặt mảnh bìa đó lên một giá nhọn tại trọng tâm G thì thấy mảnh bìa thăng bằng.
CM
5 tháng 5 2017
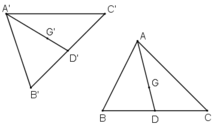
Gọi f là phép dời hình biến tam giác ABC thành tam giác A’B’C’.
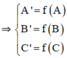
Gọi D là trung điểm của BC, D’ = f(D).
Gọi G là trọng tâm ΔABC, G’ = f(G).
+ B, D, C thẳng hàng ⇒ B’; D’; C’ thẳng hàng.
+ A; G; D thẳng hàng ⇒ A’; G’; D’ thẳng hàng.
+ B’D’ = BD = BC/2 = B’C’/2 ⇒ D’ là trung điểm B’C’.
+ A’G’ = AG = 2.AD/3 = 2.A’D’/3 ⇒ G’ là trọng tâm ΔA’B’C’.
Vậy phép dời hình f biến trọng tâm G của ΔABC thành trọng tâm G’ của ΔA’B’C’ (đpcm).
Q
31 tháng 3 2017
Gọi phép dời hình đó là f. Do f biến các đoạn thẳng AB, AC tương ứng thành các đoạn thẳng A'B', A'C' nên nó cũng biến các trung điểm M, N của các đoạn thẳng AB, AC tương ứng theo thứ tự thành các trung điểm M', N' của các đoạn thẳng A'B', A'C'. Vậy f biến các trung tuyến CM, BN của tam giác ABC tương ứng thành các trung tuyến C'M', B'N' của tam giác A'B'C'. Từ đó suy ra f biến trọng tâm G của tam giác ABC của CM và BN thành trọng tâm G' của tam giác A'B'C' là giao của C'M' và B'N'.
31 tháng 3 2017
Gọi phép dời hình đó là f. Do f biến các đoạn thẳng AB, AC tương ứng thành các đoạn thẳng A'B', A'C' nên nó cũng biến các trung điểm M, N của các đoạn thẳng AB, AC tương ứng theo thứ tự thành các trung điểm M', N' của các đoạn thẳng A'B', A'C'. Vậy f biến các trung tuyến CM, BN của tam giác ABC tương ứng thành các trung tuyến C'M', B'N' của tam giác A'B'C'. Từ đó suy ra f biến trọng tâm G của tam giác ABC của CM và BN thành trọng tâm G' của tam giác A'B'C' là giao của C'M' và B'N'.
5 tháng 9 2023
a: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BD vuông góc AB
=>BD//CH
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC vuông góc CD
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
=>BC cắt HD tại trung điểm của mỗi đường
=>I là trung điểm của HD
Xét ΔHDA có
I,O lần lượt là trung điểm của DH,DA
=>IO là đường trung bình
=>IO//AH và IO=AH/2
=>AH=2IO
Mình làm theo cách này hơi dài. Mình có đặt thêm điểm và tạo nhiều hình để làm. Có gì sai sót thông cảm nhé
Cho tam giác ABC nhọn có M,N lần lượt là trung điểm BC và AC. Đường thằng vuông góc với AB kẻ từ B và đường thăng vuông góc với AC kẻ từ C cắt nhau tại D. Gọi H là trực tâm, G là trọng tâm, O là tâm đường tròn ngoại tiếp tam giác ABC
Giải:
Bạn là CTV nên mình chỉ ghi ý chính thôi
Chứng minh H,M,D thẳng hàng và MH=MD
Do G là trọng tâm tam giác ABC nên
\(\frac{AG}{AM}=\frac{2}{3}\)
M là trung điểm HD
Nên G cũng là trọng tâm tam giác AHD (*)
Xét tam giác ACD có NA=ND
NO//CD
=> O là trung điểm AD
=> HO là trung tuyếntam giác AHD(**)
Từ (*) và (**) => H,G,O thẳng hàng
Làm kinh tinh cái gì z