Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
tổng hai góc kề bù là 180 độ suy ra góc xOy=30 độ góc yOy'=150 độ
Vì góc xoy và xoy' là 2 góc kề bù và góc xoy bằng 1/5 xoy' nên góc xoy nhỏ hơn góc xoy'
=> tia oy nằm giữa hai tia oy' và ox và góc xoy' bằng 180 độ.
=> xoy=180.1/5=36 độ
Vì tia oy nằm giữa hai tia oy' và ox , nên:
xoy+yoy'=xoy'
36+yoy'=180
yoy'=180-36
yoy'=144 độ
=>yoy'=144 độ
xoy=36 độ
Ta có : xOy = 1/5 yOy
=> xOy/1 = yOy/5 = (xOy + yOy)/(1+5) = 180/6 = 30
=> xOy = 30 độ ; yOy = 150 độ
Sửa đề: cho 2 góc kề bù xOy và yOy'.Biết xOy = 1/5yOy' . Tính số đo các góc xOy và yOy'
Ta có:\(\widehat{xOy}=\frac{1}{5}\widehat{yOy}\Rightarrow\widehat{yOy}=\widehat{xOy}:\frac{1}{5}=5\widehat{xOy}\)
Mặt khác \(\widehat{xOy}+\widehat{yOy'}=180^0\)(kề bù)
\(\Rightarrow\widehat{xOy}+5\widehat{xOy}=180^0\)
\(\Rightarrow6\widehat{xOy}=180^0\)
\(\Rightarrow\widehat{xOy}=180^0:6=30^0\)
\(\Rightarrow\widehat{yOy'}=5.30^0=150^0\)
Đáp án là A
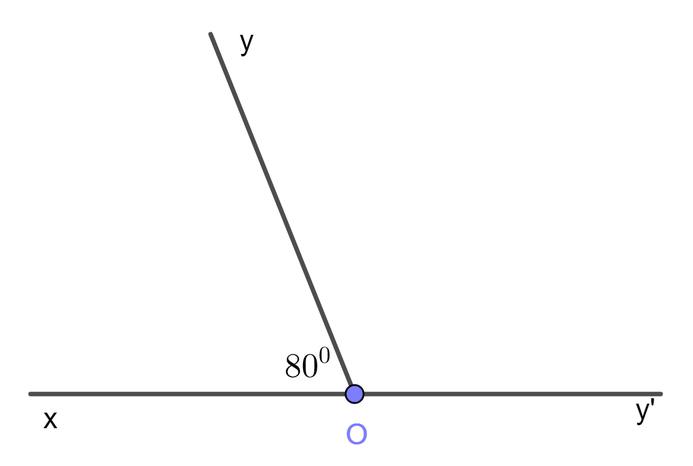
Vì ∠xOy và ∠yOy' là hai góc kề bù nên ta có: ∠xOy + ∠yOy' = 180 0 ⇒ ∠yOy' = 180 0 - 80 0 = 100 0
Đáp án là A
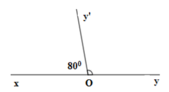
Vì ∠xOy và ∠yOy' là hai góc kề bù nên ta có: ∠xOy + ∠yOy' = 180 0 ⇒ ∠yOy' = 180 0 - 80 0 = 100 0
vì xoy và yoy' kề bù nên
xoy+yoy'=180 độ
mà xoy=60 độ
thay 60 độ+yoy'=180 độ
yoy'=120 độ
VÌ XOY VÀ YOY' LÀ HAI GÓC KỀ BÙ NÊN:
XOY + YOY' = \(180^0\)
<=> \(60^0\)+ YOY' = \(180^0\)
=> YOY' = 180 - 60 = \(120^0\)
D
D. 35 độ bạn nhé