Giải hệ phương trình :
xy =12
x - 2y -2 =0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 1 2018
Cách 1
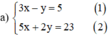
Từ (1) ta rút ra được y = 3x – 5 (*)
Thế (*) vào phương trình (2) ta được :
5x + 2(3x – 5) = 23 ⇔ 5x + 6x – 10 = 23 ⇔ 11x = 33 ⇔ x = 3.
Thay x = 3 vào (*) ta được y = 3.3 – 5 = 4.
Vậy hệ phương trình có nghiệm duy nhất (3 ; 4).
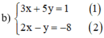
Từ (2) ta rút ra được y = 2x + 8 (*)
Thế (*) vào phương trình (1) ta được :
3x + 5(2x + 8) = 1 ⇔ 3x + 10x + 40 = 1 ⇔ 13x = -39 ⇔ x = -3.
Thay x = - 3 vào (*) ta được y = 2.(-3) + 8 = 2.
Vậy hệ phương trình có nghiệm duy nhất (-3 ; 2).
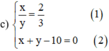
Từ (1) ta rút ra được x = 2 3 y (*)
Thế (*) vào phương trình (2) ta được :
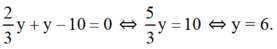
Thay y = 6 vào (*) ta được x = 4.
Vậy hệ phương trình có nghiệm duy nhất (x ; y) = (4 ; 6).
Cách 2
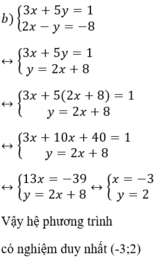
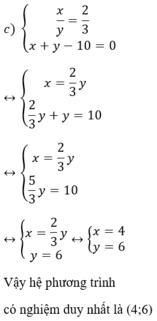
Kiến thức áp dụng
+ Giải hệ phương trình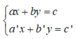 
ta làm như sau:
Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn).
Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương .
Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.
+ Nếu xuất hiện phương trình dạng 0x = a (hoặc 0y = a) thì ta kết luận hệ phương trình vô nghiệm nếu a ≠ 0 hoặc hệ có vô số nghiệm nếu a = 0.
LD
20 tháng 11 2018
Gợi ý này bây bê
Lấy pt (1) nhân với 2 rồi nhân chia cộng trừ các kiểu với pt (2)
Từ đó rồi blblblblbll sẽ tìm đc mqh x vs y
Tự túc
26 tháng 6 2020
\(\hept{\begin{cases}3x^2-2y^2-xy+12x-17y-15=0\left(1\right)\\\sqrt{2-x}+\sqrt{6-x-x^2}=y+\sqrt{2y+5}-\sqrt{y+4}\left(2\right)\end{cases}}\)
PT (1) \(\Leftrightarrow3x^2-x\left(y-12\right)-2y^2-17y-15=0\)
\(\Leftrightarrow\Delta=\left(y-12\right)^2+4\cdot3\cdot\left(2y^2+17y+15\right)\)
\(\Leftrightarrow\Delta=y^2-24y+144+24y^2+204y+180\)
\(\Leftrightarrow\Delta=25y^2+180y+324\)
\(\Delta=\left(5y+18\right)^2\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{y-12+5y+18}{3}=2y+2\\x=\frac{y-12-5y-18}{3}=\frac{-4y}{3}-10\end{cases}}\)
\(x=2y+2\)
\(\Leftrightarrow\sqrt{2-x}+\sqrt{6-x-x^2}=y+\sqrt{2y+5}-\sqrt{y+4}\)
\(\Leftrightarrow\sqrt{-2y}+\sqrt{6-2y-2-4y^2-8y-4}=y+\sqrt{2y+5}-\sqrt{y+4}\)
\(\Leftrightarrow\sqrt{-2y}+\sqrt{-4y^2-10y+0}=y+\sqrt{2y+5}-\sqrt{y+6}\)
\(\Leftrightarrow y=0\Rightarrow x=2\)
Vậy (x;y)=(2;0)
21 tháng 5 2021
\(\left\{{}\begin{matrix}xy+3y^2+x=3\left(1\right)\\x^2+xy-2y^2\left(2\right)\end{matrix}\right.\)
\(pt\left(2\right)\Leftrightarrow\left(x^2-y^2\right)+y\left(x-y\right)=0\Leftrightarrow\left(x-y\right)\left(x+2y\right)=0\Leftrightarrow\left[{}\begin{matrix}x=y\\x=-2y\end{matrix}\right.\)
+) Với x=y, thay vào pt (1) ta có: \(4x^2+x-3=0\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{3}{4}\end{matrix}\right.\)
=> \(x=y=-1;x=y=\dfrac{3}{4}\)
+) Với \(x=-2y\), thay vào pt(1) ta có: \(y^2-2y-3=0\Leftrightarrow\left[{}\begin{matrix}y=-1\Rightarrow x=2\\y=3\Rightarrow x=-6\end{matrix}\right.\)
Vậy hpt có 4 nghiệm: \(\left(x;y\right)\in\left\{\left(-1;-1\right),\left(\dfrac{3}{4};\dfrac{3}{4}\right),\left(2;-1\right),\left(-6;3\right)\right\}\)
AH
Akai Haruma
Giáo viên
6 tháng 8 2021
Lời giải:
a.
$x^2-x=y^2-1$
$\Leftrightarrow x^2-x+1=y^2$
$\Leftrightarrow 4x^2-4x+4=4y^2$
$\Leftrightarrow (2x-1)^2+3=(2y)^2$
$\Leftrightarrow 3=(2y)^2-(2x-1)^2=(2y-2x+1)(2y+2x-1)$
Đến đây xét các TH:
TH1: $2y-2x+1=1; 2y+2x-1=3$
TH2: $2y-2x+1=-1; 2y+2x-1=-3$
TH3: $2y-2x+1=3; 2y+2x-1=1$
TH4: $2y-2x+1=-3; 2y+2x-1=-1$
b.
$x^2+12x=y^2$
$\Leftrightarrow (x+6)^2=y^2+36$
$\Leftrightarrow 36=(x+6)^2-y^2=(x+6-y)(x+6+y)$
Đến đây xét trường hợp tương tự phần a.
c.
$x^2+xy-2y-x-5=0$
$\Leftrightarrow x^2+xy=x+2y+5$
$\Leftrightarrow 4x^2+4xy=4x+8y+20$
$\Leftrightarrow (2x+y)^2=4x+8y+20+y^2$
$\Leftrightarrow (2x+y)^2-2(2x+y)+1=y^2+6y+21$
$\Leftrightarrow (2x+y-1)^2=(y+3)^2+12$
$\Leftrightarrow (2x+y-1)^2-(y+3)^2=12$
$\Leftrightarrow (2x+y-1-y-3)(2x+y-1+y+3)=12$
$\Leftrightarrow (2x-4)(2x+2y+2)=12$
$\Leftrightarrow (x-2)(x+y+1)=3$
Đến đây đơn giản rồi.
8 tháng 8 2021
a) \(x^2-x=y^2-1\)
\(\Rightarrow x^2-x+1=y^2\)
\(\Rightarrow4x^2-4x+4=4y^2\)
\(\Rightarrow4x^2-4x+1+3=\left(2y\right)^2\)
\(\Rightarrow\left(2x+1\right)^2-\left(2y\right)^2=-3\)
\(\Rightarrow\left(2x-2y+1\right)\left(2x+2y+1\right)=-3\)
Vì \(x,y\in Z\Rightarrow\left\{{}\begin{matrix}\left(2x-2y+1\right)\left(2x+2y+1\right)\in Z\\\left(2x-2y+1\right)\left(2x+2y+1\right)\inƯ\left(7\right)\end{matrix}\right.\)
Ta có bảng:
| x-y | -1 | 0 | -2 | 1 |
| x+y | 1 | -2 | 0 | -1 |
| x | 0 | -1 | -1 | 0 |
| y | 1 | -1 | -1 | -1 |
Vậy \(\left(x,y\right)\in\left\{\left(0;1\right);\left(-1;-1\right);\left(-1;-1\right);\left(0;-1\right)\right\}\)
13 tháng 12 2020
\(\left\{{}\begin{matrix}x^3+xy^2+3\left(x-2y\right)=0\\x^2+xy=3\end{matrix}\right.\)\(\Rightarrow x^3+xy^2+\left(x^2+xy\right)\left(x-2y\right)=0\)\(\Leftrightarrow x^3+xy^2+x^3-x^2y-2xy^2=0\Leftrightarrow2x^3-x^2y-xy^2=0\)\(\Leftrightarrow x\left(2x+y\right)\left(x-y\right)=0\)\(\Leftrightarrow\left[{}\begin{matrix}x=0\\y=-2x\\x=y\end{matrix}\right.\)
+) \(x=0\Rightarrow0y=3\)(vô nghiệm)
+) y=-2x \(\Rightarrow x^2-2x^2=3\Leftrightarrow-x^2=3\)(vô nghiệm)
+) x=y\(\Rightarrow2x^2=3\Leftrightarrow x^2=\dfrac{3}{2}\Leftrightarrow\left[{}\begin{matrix}x=y=\sqrt{\dfrac{3}{2}}\\x=y=-\sqrt{\dfrac{3}{2}}\end{matrix}\right.\)
\(\hept{\begin{cases}xy=12\\x-2y-2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{12}{y}\\\frac{12}{y}-2y=2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=\frac{12}{y}\\\frac{12}{y}-\frac{2y^2}{y}=2\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{12}{y}\\\frac{12-2y^2}{y}=2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=\frac{12}{y}\\12-2y^2-2y=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{12}{y}\\y^2+y-6=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y^2+2.\frac{1}{2}y+\frac{1}{4}-\frac{1}{4}-6=0\\x=\frac{12}{y}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(y+\frac{1}{2}\right)^2-\frac{25}{4}=0\\x=\frac{12}{y}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(y+\frac{1}{2}-\frac{5}{2}\right)\left(y+\frac{1}{2}+\frac{5}{2}\right)=0\\x=\frac{12}{y}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(y-2\right)\left(y+3\right)=0\\x=\frac{12}{y}\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}y=2\\y=-3\end{cases}}\) và \(x=\frac{12}{y}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{12}{2}\\x=\frac{12}{-3}\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=6\\x=-4\end{cases}}\)
vậy \(\orbr{\begin{cases}y=2\\y=-3\end{cases}}\) và \(\orbr{\begin{cases}x=6\\x=-4\end{cases}}\)