NÊU ĐỊNH LÝ PY-TA-GO . VẼ HÌNH MINH HỌA VÀ NÊU GIẢ THIẾT KẾT LUẬN.
CÁC BN GIÚP MIK NHA , KO CẦN NÊU ĐỊNH LÝ CX ĐC. MIK CẦN GẤP LẮM !
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 1 2023
Tổng ba góc trong 1 tam giác bằng 180 độ
| GT | ΔABC |
| KL | góc A+góc B+góc C=180 độ |
10 tháng 1 2023
a:
| GT | góc AOB và góc COD là hai góc đối đỉnh |
| KL | góc AOB=góc COD |
b:
| GT | a\(\perp\)b, c\(\perp\)b |
| KL | a//c |
HI
3
CW
29 tháng 5 2016
Thuận:
Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương 2 cạnh góc vuông.
Đảo:
Tam giác có bình phương 1 cạnh bằng tổng bình phương 2 cạnh còn lại là tam giác vuông.
Có thể ko chính xác từng chữ (do lười học bài cũ), bạn thông cảm nhé ^^!
29 tháng 5 2016
Thuận:
Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông
Đảo:
Trong một tam giác, nếu có bình phương một cạnh bẳng tổng bình phương hai cạnh còn lại thì tam giác đó là tam giác vuông
Nếu mình nhớ ko nhầm thì hình như hai định lý được phát biểu như thế này. Nếu có gì sai xin các bạn thông cảm
HN
26 tháng 2 2018
-tam giác cân:+2 cạnh bằng nhau, hai góc ở đáy bằng nhau
+Tam giác có đường cao kẻ từ đỉnh là phân giác(trung tuyến, trung trực)
+Tam giác có phân giác kẻ từ đỉnh là đường cao (trung trực, trung tuyến)
+Tam giác có đường trung trực kẻ từ đỉnh là phân giác (trung tuyến, đường cao)
+Tam giác có đường trung tuyến kẻ từ đỉnh là trung trực( phân giác, đường cao)
+Tam giác có một đường trung trực kẻ từ đỉnh
26 tháng 2 2018
cm:1 tam giác là tam giác cân:
-2 cạnh bằng nhau, hai góc ở đáy bằng nhau
-Tam giác có đường cao kẻ từ đỉnh là phân giác(trung tuyến, trung trực)
-Tam giác có phân giác kẻ từ đỉnh là đường cao (trung trực, trung tuyến)
-Tam giác có đường trung trực kẻ từ đỉnh là phân giác (trung tuyến, đường cao)
- Tam giác có đường trung tuyến kẻ từ đỉnh là trung trực( phân giác, đường cao)
- Tam giác có một đường trung trực kẻ từ đỉnh
cm 1 tam giác là tam giác đều:
* tam giác đều
- chứng minh tam giác có 3 cạnh = nhau
- chứng minh tam giác có 3 góc = nhau
- chứng minh tam giác có 2 góc = 60*
- chứng minh tam giác cân có 1 góc = 60*
NP
2
10 tháng 11 2021
Tham khảo!
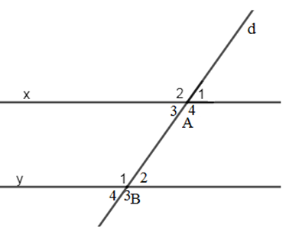
Giả thiết: Đường thẳng cắt hai đường thẳng sao cho có một góc so le trong bằng nhau.
Kết luận: Hai đường thẳng đó song song.
Định lý Pytago: trong một tam giác vuông, tổng bình phương 2 cạnh góc vuông bằng bình phương cạnh huyền.
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
∆ABC vuông tại A.
=> BC2=AB2+AC2
Tham khảo nhé:
Câu hỏi của Uyên Trần - Toán lớp 7 - Học toán với OnlineMath