Chứng minh rằng: Nếu độ dài các cạnh của tam giác liên hệ với nhau bởi bất đẳng thức \(^{a^2+b^2>5c^2}\)thì c là độ dài cạnh nhỏ nhất của tam giác.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giả sử c không phải là cạnh nhỏ nhất,chẳng hạn \(a\le c\).
Khi đó:\(a^2\le c^2\)và \(b^2\le\left(a+c\right)^2\le4c^2\)
\(\Rightarrow a^2+b^2< 5c^2\)(trái với giả thiết)
\(\Rightarrow\)điều giả sử sai
\(\Rightarrow\)điều ngược lại đúng,tức là c là độ dài cạnh nhỏ nhất của tam giác.

Xét tam thức f(x) = b2x2 - (b2 + c2 - a2)x + c2 có:
Δ = (b2 + c2 - a2)2 - 4b2c2
= (b2 + c2 - a2 - 2bc)(b2 + c2 - a2 + 2bc)
= [(b - c)2 - a2][(b + c)2 - a2]
= (b – c – a)(b – c + a)(b + c + a)(b + c – a).
Do a, b, c là 3 cạnh của tam giác nên theo bất đẳng thức tam giác ta có:
b < c + a ⇒ b – c – a < 0
c < a + b ⇒ b – c + a > 0
a < b + c ⇒ b + c – a > 0
a, b, c > 0 ⇒ a + b + c > 0
⇒ Δ < 0 ⇒ f(x) cùng dấu với b2 ∀x hay f(x) > 0 ∀x (đpcm).

Gọi độ dài ba cạnh của tam giác theo thứ tự từ nhỏ đến lớn là x,y,z (tính bằng m)
(x > 0; y > 0 và z > 6)
* Cạnh lớn nhất dài hơn cạnh nhỏ nhất là 6m nên: z - x = 6
Vì 3 cạnh của tam giác tỉ lệ với 3,4,5 nên ta có:
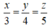
Theo tính chất dãy tỉ số bằng nhau ta có:
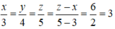
x/3 = 3 ⇒ x = 3.3 = 9
y/4 = 3 ⇒ y = 4.3 = 12
z/5 = 3 ⇒ z = 5.3 = 15
Vậy độ dài 3 cạnh của tam giác là 9m; 12m; 15m

Gọi độ dài 3 cạnh tam giác lần lượt là x;y;z
Do độ dài các cạnh tỉ lệ với 3;5;7 nên: \(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{7}\)
Do cạnh lớn nhất dài hơn cạnh nhỏ nhất 40m nên: \(z-x=40\)
Áp dụng tính chất tỉ lệ thức:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{7}=\dfrac{z-x}{7-3}=\dfrac{40}{4}=10\)
\(\Rightarrow\left\{{}\begin{matrix}x=3.10=30\\y=5.10=50\\z=7.10=70\end{matrix}\right.\)
Vậy độ dài 3 cạnh tam giác là 30m, 50m, 70m

gọi độ dài các cạnh lần lượt là a,b,c ( a<b<c)
Ta có a/3=c/5
Áp dụng t/c dãy tỉ số bằng nhau ta có
a/3=c/5=c-a/5-3= 8/2=4
=> a= 4x3= 12
c= 4x5=20
b/4=4 => b=4x4=16
Giả sử c không là độ dài cạnh nhỏ nhất, không mất tính tổng quát, giả sử : \(c\ge a\)
\(\Rightarrow c^2+b^2\ge a^2+b^2>5c^2\)
\(\Rightarrow b^2>4c^2=\left(2c\right)^2\)(1)
Vì b và c là số dương (độ dài các cạnh) nên \(\left(1\right)\Leftrightarrow b>2c\ge c+a\)(trái với bđt tam giác)
Vậy điều giả sử là sai nên c là độ dài cạnh nhỏ nhất (đpcm)