giải phương trình ngiệm nguyên 1) \(x^2y^2-xy=x^2+2y^2\) 2) \(2^x+3^x=5^x\) 3)\(\left(2x+5y+1\right)\) (2/x/+y+x2+x)=105
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có
\(x^4+y^4=7z^4+5\Leftrightarrow x^4+y^4+z^4=8z^4+5\)
Áp dụng tính chất lũy thừa bậc 4 của số nguyên a khi chia cho 8 dư 0 hoặc 1
tức là \(a^4\equiv0,1\left(mod8\right)\)
\(\Rightarrow a^4+b^4+c^4\equiv0,1,2,3\left(mod8\right)\)
Mà \(8z^4+5\equiv5\left(mod8\right)\)
vậy pt k có nghiệm nguyên

Ta đặt:
\(\sqrt{x-2009}=a\)
\(\sqrt{y-2010}=b\)
\(\sqrt{z-2011}=c\)
Với a ; b ; c >0 . Khi này , pt trở thành:
\(\dfrac{a-1}{a^2}+\dfrac{b-1}{b^2}+\dfrac{c-1}{c^2}=\dfrac{3}{4}\)
\(\Leftrightarrow\left(\dfrac{1}{4}-\dfrac{1}{a}+\dfrac{1}{a^2}\right)+\left(\dfrac{1}{4}-\dfrac{1}{b}+\dfrac{1}{b^2}\right)+\left(\dfrac{1}{4}-\dfrac{1}{c}+\dfrac{1}{c^2}\right)=0\)
\(\Leftrightarrow\left(\dfrac{1}{2}-\dfrac{1}{a}\right)^2+\left(\dfrac{1}{2}-\dfrac{1}{b}\right)^2+\left(\dfrac{1}{2}-\dfrac{1}{c}\right)^2=0\)
\(\Leftrightarrow a=b=c=2\)
Suy ra :
x = 2013
y = 2014
z = 2015

Ta có: x -3y =2
<=> 2x-6y =4 (1)
* 2x-5y= -1 (2)
Phương trình (1) -pt (2) ta có:
2x -6y -(2x-5y) =4-(-1)
<=> 2x- 6y -2x+5y =5
<=>y= -5
Thay y= -5 vào pt (2) ta có:
2.x -5.(-5) =-1
<=>2x +25 =-1
<=> 2x=-26
<=> x=-13

\(\left\{{}\begin{matrix}x^2+y^2+6x+2y=0\\x+y+8=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+\left(x+8\right)^2+6x-2\left(x+8\right)=0\\y=-x-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+10x+24=0\\y=-x-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=-4\\x=-6\end{matrix}\right.\\y=-x-8\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=-4\\y=-4\end{matrix}\right.\\\left\{{}\begin{matrix}x=-6\\y=-2\end{matrix}\right.\end{matrix}\right.\)
Kết luận: Hệ phương trình đã cho có nghiệm \(\left(x;y\right)\in\left\{\left(-4;-4\right);\left(-6;-2\right)\right\}\)

\(x^2-xy+y^2=3\)
\(\Leftrightarrow2x^2-2xy+2y^2=6\)
\(\Leftrightarrow\left(x-y\right)^2+x^2+y^2=1+1+4\)
\(\Rightarrow\left(\left(x-y\right)^2,x^2,y^2\right)=\left(1,1,4;1,4,1;4,1,1\right)\)
\(\Rightarrow\left(x,y\right)=\left(-1,-2;1,2;2,1;-2,-1;-1,1;1,-1\right)\)

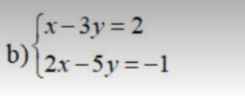 giải hệ phương trình
giải hệ phương trình