Tìm các số nguyên n sao cho biểu thức sau là số nguyên: 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để P là số nguyên thì \(n-1\in\left\{1;-1\right\}\)
hay \(n\in\left\{2;0\right\}\)

Ta có: \(P=\frac{2n-1}{n-1}=\frac{2n-2+1}{n-1}=\frac{2\left(n-1\right)+1}{n-1}=2+\frac{1}{n-1}\)
Để P là số nguyên thì \(1⋮n-1\)\(\Rightarrow n-1\inƯ\left(1\right)=\left\{-1;1\right\}\)
\(\Rightarrow n\in\left\{1;2\right\}\)
mà \(n\ne1\)\(\Rightarrow n=2\)
Vậy n = 2
ta có n-1 / hết cho n-1 , 2n chia hết cho n, gọi n-1 =k . 2n-1 = 2k ta có 2k/k=k và k thuộc B2 vậy ta có bội 2 chia hết cho k nên phải gấp đô k nên k là một sô bất kì vậy n nên n cx là một số bất kì

Q=3n+1n−1=3n−3+5n−1=3n−3n−1+1n−1=3+1n−1P=3n+2n−1=3n−3+5n−1=3n−3n−1+5n−1=3+5n−1
⇒1⋮n−1⇔n−1∈
(1)={±1;±3}⇒5⋮n−1⇔n−1∈Ư(5)={±1;±5}
⇒⎡⎢ ⎢ ⎢⎣n−1=1n−1=−1n−

\(B\inℤ\Rightarrow2B\inℤ\Rightarrow\frac{2n}{2n-1}=\frac{2n-1+1}{2n-1}=1+\frac{1}{2n-1}\inℤ\)
\(\Rightarrow\frac{1}{2n-1}\inℤ\Leftrightarrow2n-1\in\left\{-1,1\right\}\Leftrightarrow n\in\left\{0,1\right\}\).
Thử lại ta đều thấy thỏa mãn.
\(\text{Để B nguyên thì }:n⋮2n-1\)
\(\text{vì}:n⋮2n-1\)\(\text{nên}:2n+0⋮2n-1\)
\(\left(2n-1\right)+1⋮2n-1\)
Vì \(\left(2n-1\right)⋮2n-1\)
nên \(1⋮2n-1\)
suy ra \(2n-1\inƯ\left(1\right)=\pm1\)
với 2n-1=1 hoặc 2n-1=-1
2n=2 2n=0
n=1 n=0
vậy n=0 hoặc n=1 thì thỏa mãn điều kiện trên

Để P nguyên thì 2n - 1 ⋮ n - 1
<=> 2n - 2 + 1 ⋮ n - 1
<=> 2( n - 1 ) + 1 ⋮ n - 1
Vì 2( n - 1 ) ⋮ n - 1
=> 1 ⋮ n - 1
=> n - 1 thuộc Ư(1) = { 1; -1 }
=> n thuộc { 2; 0 }
chẹm tao cho lắm cần tao banh lồn cho mày chịch để tao làm phim sex không tao là tokuda đây nhưng tui là tokuda nữ

22/ a/ 0;-2;4;6;-6;-4..........
b/ 1;-1;3;5;
23/ a/ -21/28=-3/4;-39/52=-3/4
=> -21/28=-39/52
b/ -171717/232323=-17/23
=>.....

giúp mik nhoa mik đag cần cảm ơn những câu hỏi của tất cả các bn nhiều![]()

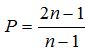
P thuộc Z <=> (2n1-1) chia hết cho (n-1)
<=> (2n-2+1) chia hết cho (n-1)
<=> [(2n-2)+1] chia hết cho (n-1)
<=> [2(n-1)+1] chia hết cho (n-1)
Vì 2(n-1) chia hết cho (n-1)
=> P thuộc Z <=> 1 chia hết cho n-1
<=> n-1 thuộc Ư(1)
<=> n-1=1
hoặc n-1=-1
<=> n=2
hoặc n=0
Vậy P thuộc Z <=> n thuộc {2;0}
Thấy đúng nhớ k cho mình nha
Ta có : \(\frac{2n-1}{n-1}=\frac{2}{n-1}.\frac{n-1}{n-1}=\frac{2}{n-1}.1\)
Vì \(1\in Z\)nên \(\frac{2}{n-1}\in Z\)
\(\Rightarrow n-1\in\)Ư(2)
Ư(2) = { -2;-1;1;2}
Ta có bảng sau :
Vậy \(n\in\left\{-1;0;2;3\right\}\)