hai đường MN và PQ cắt nhau tại A. Biết MAQ+NAP=250o. tính số góc NAP
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
26 tháng 8 2017
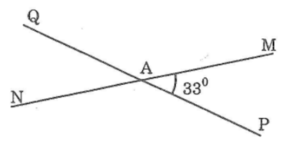
∠PAM và ∠MAQ là hai góc kề bù nên ∠PAM + ∠MAQ=180o
Suy ra: ∠MAQ = 180o-∠PAM =180o-33o=147o
PT
1
CM
3 tháng 4 2019
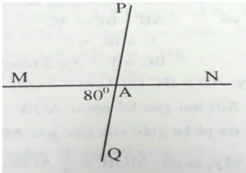
Ta có: ∠MAQ và ∠MAP kề bù nên:
∠MAQ + ∠MAP = 180 0
80 0 + ∠MAP = 180 0
∠MAP = 180 0 - 80 0 = 100 0
Và ∠MAP và ∠PAN kề bù nên:
∠MAP + ∠PAN = 180 0
100 0 + ∠PAN = 180 0
∠PAN = 180 0 - 100 0 = 80 0
CM
28 tháng 1 2017
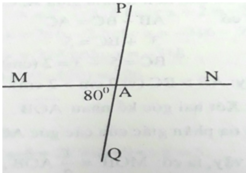
Ta có: M A Q ^ và M A P ^ kề bù nên:
M A Q ^ + M A P ^ = 180 °
80 ° + M A P ^ = 180 °
M A P ^ = 180 ° - 80 ° = 100 °
Và M A P ^ và P A N ^ kề bù nên:
M A P ^ + P A N ^ = 180 °
100 ° + P A N ^ = 180 °
P A N ^ = 180 ° - 100 ° = 80 °
26 tháng 9 2021
a) Ta có:
∠MAP= ∠NAQ (hai góc đối đỉnh)
⇒ ∠NAQ = 45o
⇒ ∠NAQ = 45o
b) Ta có:
∠MAP + ∠MAQ = 180o ( hai góc kề bù )
⇒ 45o + ∠MAQ = 180o
⇒ ∠MAQ = 180o − 45o = 135o
c) Các cặp góc đối đỉnh là:
∠MAP, ∠NAQ
∠NAP, ∠MAQ
d) Các cặp góc bù nhau là:
∠MAP, ∠NAP
∠MAP, ∠MAQ
∠NAQ, ∠NAP
∠NAQ, ∠MAQ
20 tháng 9 2016
a,có góc NAQ= goc MAP hai góc đối đỉnh
mà góc MAP =33 độ
suy ra góc NAQ=33 độ b, có gocsMAP+goc MAQ=180 hai goc ke bu goc
MAQ=180‐33=147 độ c, MAP va QAN QAM va NAP d, MAP va MAQ QAN va NAP
18 tháng 4 2018
a. Ta có:
∠NAQ và ∠PAM là hai góc đối đỉnh
Suy ra:∠NAQ = CPAM
mà ∠PAM = 33o nên ∠NAQ = 33o
b. ∠PAM và ∠MAQ là hai góc kề bù nên ∠PAM + ∠MAQ=180o
Suy ra: ∠MAQ = 180o-∠PAM =180o-33o=147o
c. Các cặp góc đối đỉnh là: ∠PAM và ∠NAQ ; ∠PAN và ∠MAQ
d. Các cặp góc kề bù là: ∠PAM và ∠MAQ; ∠PAM và ∠PAN ; ∠NAQ và ∠PAN ; ∠NAQ và ∠QAM
18 tháng 4 2018
a. Ta có:
∠NAQ và ∠PAM là hai góc đối đỉnh
Suy ra:∠NAQ = CPAM
mà ∠PAM = 33o nên ∠NAQ = 33o
b. ∠PAM và ∠MAQ là hai góc kề bù nên ∠PAM + ∠MAQ=180o
Suy ra: ∠MAQ = 180o-∠PAM =180o-33o=147o
c. Các cặp góc đối đỉnh là: ∠PAM và ∠NAQ ; ∠PAN và ∠MAQ
d. Các cặp góc kề bù là: ∠PAM và ∠MAQ; ∠PAM và ∠PAN ; ∠NAQ và ∠PAN ; ∠NAQ và ∠QAM
Theo đề ra: Hai đường MN và PQ cắt nhau tại A
=> Góc MAQ = góc NAP ( đối đỉnh )
Ta có: Góc MAQ + NAP = 250 độ
=> Góc MAQ = góc NAP = 250 độ : 2
=> Góc MAQ = góc NAP = 125 độ