Tim x
3x2 +6x= 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Leftrightarrow\left(x+2\right)\left(5-3x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{5}{3}\end{matrix}\right.\)

Δ=6^2-4*3*m=36-12m
Để BPT luôn đúng khi x>=0 thì 36-12m<0
=>12m>36
=>m>3

\(a,\Leftrightarrow3x\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\\ b,\Leftrightarrow x\left(x-1\right)+2\left(x-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)

a) Cách 1: Khai triển HĐT rút gọn được 3 x 2 + 6x + 7 = 0
Vì (3( x 2 + 2x + 1) + 4 < 0 với mọi x nên giải được x ∈ ∅
Cách 2. Chuyển vế đưa về ( x + 3 ) 3 = ( x - 1 ) 3 Û x + 3 = x - 1
Từ đó tìm được x ∈ ∅
b) Đặt x 2 = t với t ≥ 0 ta được t 2 + t - 2 = 0
Giải ra ta được t = 1 (TM) hoặc t = -2 (KTM)
Từ đó tìm được x = ± 1
c) Biến đổi được ![]()
d) Biến đổi về dạng x(x - 2) (x - 4) = 0. Tìm được x ∈ {0; 2; 4}

\(a,\) PT thứ 2 bị lỗi rồi bạn, dấu '' = '' đou
\(b,\)
\(4x^2-32=0\Leftrightarrow4x^2=32\Leftrightarrow x^2=8\Leftrightarrow x=\pm\sqrt{8}\)
\(3x^2=48\Leftrightarrow x^2=16\Leftrightarrow x=\pm4\)
Vậy 2 pt trên không tường đương

\(a,6\left(x^2-2x+3\right)=2\left(3x^2-6x+9\right)\)
\(\Leftrightarrow6x^2-12x+18=6x^2-12x+18\)
\(\Leftrightarrow\) pt vô nghiệm
\(3x-6=3\left(x-2\right)\)
\(\Leftrightarrow3x-6=3x-6\)
\(\Leftrightarrow\) pt vô nghiệm
Vậy 2 pt tương đương
\(b,4x^2-32=0\Leftrightarrow x^2=8\Leftrightarrow x=\pm\sqrt{8}\)
\(3x^2=48\Leftrightarrow x=\pm4\)
Vậy 2 pt ko tương đương
Phương trình b tương đương vì chúng có cùng tập nghiệm là S={4;-4}
a: 6(x^2-2x+3)=2(3x^2-6x+9)
=>6x^2-12x+18=6x^2-12x+18
=>-12x=-12x
=>0x=0(luôn đúng)
3x-6=3(x-2)
=>3x-6=3x-6
=>0x=0(luôn đúng)
=>Hai phương trình tương đương

Điều kiện: x> -1
Ta có: 3x2- 6x+ ln( x+1) 3+1=0 hay 3x2- 6x+ 3ln( x+1)+1=0
f(x)=3x2- 6x+ 3ln( x+1) +1=0 ⇒ f ' ( x ) = 6 x - 6 + 3 x + 1
Đạo hàm f’ (x) = 0 khi và chỉ khi (2x- 2) (x+ 1) +1=0
⇔ x = ± 1 2
Từ đây, ta có bảng biến thiên của f(x):
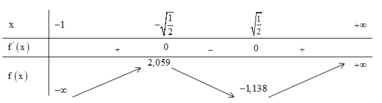
Nhìn vào bảng biến thiên ta sẽ có phương trình đã cho có 3 nghiệm phân biệt.
Chọn C.
\(3x^2+6x=0\)
\(\Rightarrow3x\left(x+2\right)=0\)
\(\Rightarrow\orbr{\begin{cases}3x=0\\x+2=0\end{cases}\Rightarrow\orbr{\begin{cases}x=0\\x=-2\end{cases}}}\)
Vậy \(x=0;-2\)
Ta có :
3x2 + 6x = 0
x . ( 3x + 6 ) = 0
\(\Rightarrow\orbr{\begin{cases}x=0\\3x+6=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=0\\3x=-6\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x=-2\end{cases}}\)