Trong mặt phẳng toạ độ Oxy cho (P)y=mx^2(m>0) và đường thẳng (d)y=2x-m^2 a) Tìm m để (d) cắt (P) tại hai điểm phân biệt A,B.Cmr A và B nằm cùng về một phía của trục tung b) Với m tìm được ở câu a.Gọi xA,xB lần lược là hoành đồ điểm A và B.Tìm m để (P)=2/(xA+xB)+1/(4xAxB+1) đạt GTNN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: 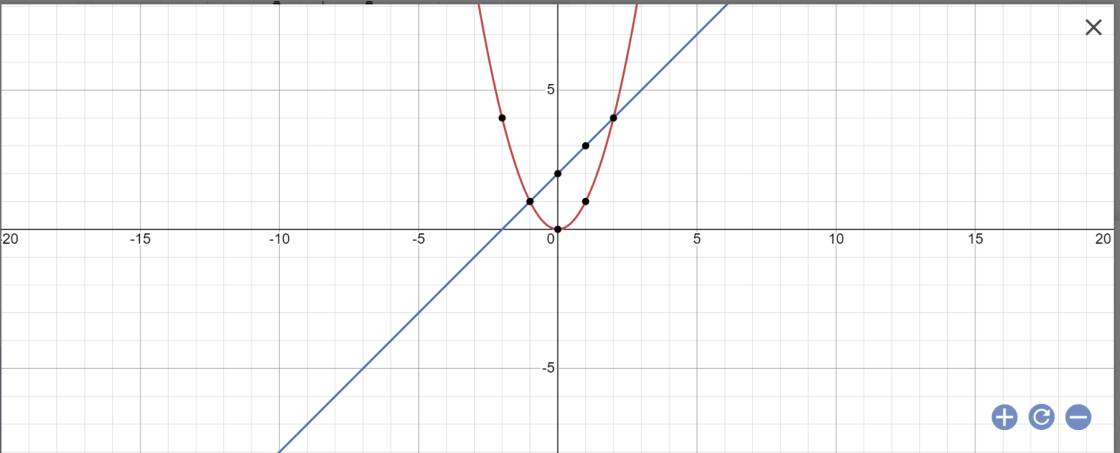
b: PTHĐGĐ là:
x^2-x-2=0
=>(x-2)(x+1)=0
=>x=2 hoặc x=-1
=>y=4 hoặc y=1
c: PTHĐGĐ là:
x^2-2x+m=0
Để (P) cắt (d1) tại hai điểm nằm về hai phía của trục tung thì m<0

b) Phương trình hoành độ giao điểm của (P) và (d):
x² = mx - m + 1
⇔ x² - mx + m - 1 = 0
∆ = m² - 4.1.(m - 1)
= m² - 4m + 4
= (m - 2)² ≥ 0 với mọi m ∈ R
⇒ Phương trình luôn có hai nghiệm
Theo Viét ta có:
x₁ + x₂ = m (1)
x₁x₂ = m - 1 (2)
Lại có x₁ + 3x₂ = 7 (3)
Từ (1) ⇒ x₁ = m - x₂ (4)
Thay x₁ = m - x₂ vào (3) ta được:
m - x₂ + 3x₂ = 7
2x₂ = 7 - m
x₂ = (7 - m)/2
Thay x₂ = (7 - m)/2 vào (4) ta được:
x₁ = m - (7 - m)/2
= (2m - 7 + m)/2
= (3m - 7)/2
Thay x₁ = (3m - 7)/2 và x₂ = (7 - m)/2 vào (2) ta được:
[(3m - 7)/2] . [(7 - m)/2] = m - 1
⇔ 21m - 3m² - 49 + 7m = 4m - 4
⇔ 3m² - 28m + 49 + 4m - 4 = 0
⇔ 3m² - 24m + 45 = 0
∆' = 144 - 3.45 = 9 > 0
Phương trình có hai nghiệm phân biệt:
m₁ = (12 + 3)/3 = 5
m₂ = (12 - 3)/3 = 3
Vậy m = 3; m = 5 thì (P) và (d) cắt nhau tại hai điểm có hoành độ thỏa mãn x₁ + 3x₂ = 7

b) (d) cắt (P) tại 2 điểm A, B phân biệt nằm về 2 phía của trục tung khi và chỉ khi
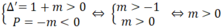
Khi đó 2 nghiệm của phương trình là:
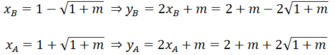
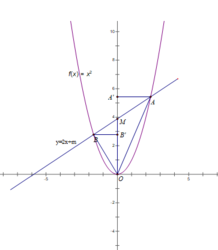
Kẻ BB' ⊥ OM ; AA' ⊥ OM
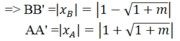
Ta có:
S A O M = 1/2 AA'.OM ; S B O M = 1/2 BB'.OM
Theo bài ra:
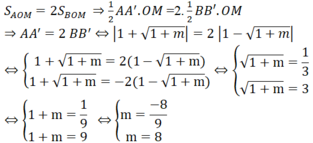
Do m > 0 nên m = 8
Vậy với m = 8 thì thỏa mãn điều kiện đề bài.

a, Biến đổi hệ phương trình ban đầu ta được hệ x - y = 0 3 x + 3 y = 12
Từ đó tìm được x = 2, y = 2
b, Phương trình hoành độ giao điểm của d và (p):
x 2 - 2 x - m 2 + 2 m = 0 (1)
d cắt (P) tại hai điểm phân biệt nằm về hai phía của trục tung Oy <=> (1) có hai nghiệm trái dấu. Từ đó tìm được 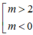
Kết luận 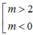

a: Thay x=1 và y=3 vào (d), ta được:
m+3-m=3
=>3=3(luôn đúng)
b: PTHĐGĐ là:
x^2-mx-3+m=0
=>x^2-mx+m-3=0
Để (d) cắt (P) tại hai điểm phân biệt thì m-3<0
=>m<3


Xét phương trình hoành độ ta có :\(mx^2-2x+m^2=0\)
\(\Delta=b^2-4ac=4-4m^3\)
Để phương trình có nghiệm thì \(\Delta\ge0\)hay \(4-4m^3\ge0\)
\(4\ge4m^3\)
\(1\ge m^3\)
\(1\ge m\)
Theo Vi-ét ta có \(\hept{\begin{cases}xA+xB=\frac{-b}{a}=\frac{2}{m}\\xAxB=\frac{c}{a}=m\end{cases}}\)
Vì m >0 nên \(xAxB>0\)
Vậy phương trình có hai nghiệm cùng dấu nên A B nằm cùng 1 phía trục tung
Ta có :\(\frac{2}{xA+xB}+\frac{1}{4xAxB+1}\)
\(\frac{2}{\frac{2}{m}}\)\(+\frac{1}{4m+1}\)= \(m+\frac{1}{4m+1}=\frac{m\left(4m+1\right)}{4m+1}+\frac{1}{4m+1}\)=\(\frac{4m^2+m+1}{4m+1}=P\)
\(4m^2+m+1=P\left(4m+1\right)\)
\(4m^2+m+1=4mP+P\)
\(4m^2+m+1-4mP-P=0\)
\(4m^2+m-4mP+1-P=0\)
\(4m^2+m\left(1-4P\right)+1-P=0\)
\(\Delta=b^2-4ac=\left(1-4P\right)^2-16\left(1-P\right)\)
\(=1-8P+16P^2-16+16P\)
\(=-15+8P+16P^2\)
Để phương trình có nghiệm thì \(\Delta\ge0\)hay \(16P^2+8P-15\ge0\)
\(\orbr{\begin{cases}P\le\frac{-5}{4}\\P\ge\frac{3}{4}\end{cases}}\)
Vậy minP =\(\frac{3}{4}\)
Dấu = xảy ra \(< =>\)\(\frac{4m^2+m+1}{4m+1}=P\)
\(\frac{4m^2+m+1}{4m+1}=\frac{3}{4}\)
\(4\left(4m^2+m+1\right)=3\left(4m+1\right)\)
\(16m^2+4m+4-12m-3=0\)
\(16m^2-8m+1=0\)
\(m=\frac{1}{4}\)
Vậy minP=\(\frac{3}{4}\)khi và chỉ khi \(m=\frac{1}{4}\)