cho tam giác MNP vuông tại M MK vuông NP tại K treenKP lấy I sao cho NK=KI kéo dài Mk lấy Q sao choKQ=MK cm MN song song với QI
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔMKH có MK=MH
nên ΔMKH cân tại M
b: Xét ΔKMN và ΔHMP có
MK=MH
\(\widehat{KMN}=\widehat{HMP}\)
MN=MP
Do đó: ΔKMN=ΔHMP
c: Ta có: ΔMKH cân tại M
mà MQ là đường trung tuyến
nên MQ là đường cao

a: Xét ΔMKH có MK=MH
nên ΔMKH cân tại M
b: Xét ΔKMN và ΔHMP có
MK=MH
\(\widehat{KMN}=\widehat{HMP}\)
MN=MP
Do đó: ΔKMN=ΔHMP
c: Ta có: ΔMKH cân tại M
mà MQ là đường trung tuyến
nên MQ là đường cao

a: Xét ΔMKN vuông tại K và ΔPMN vuông tại M có
góc N chung
=>ΔMKN đồng dạng với ΔPMN
b: NK=căn 15^2-12^2=9cm
PK=12^2/9=16cm
PN=9+16=25cm
c: ΔMNP vuông tại M có MK là đường cao
nên NM^2=NK*NP

\(\text{#TNam}\)
`a,`
Xét Tam giác `MNP:`\(\widehat{M}=90^0\)
`-> \text {NP là cạnh lớn nhất} (\text {theo định lý giữa góc và cạnh đối diện})`
`-> MN < NP`
`b,`
Xét Tam giác `MNK: MN = MK`
`-> \text {Tam giác MNK cân tại M}`
`->`\(\widehat{MNK}=\widehat{MKN}.\)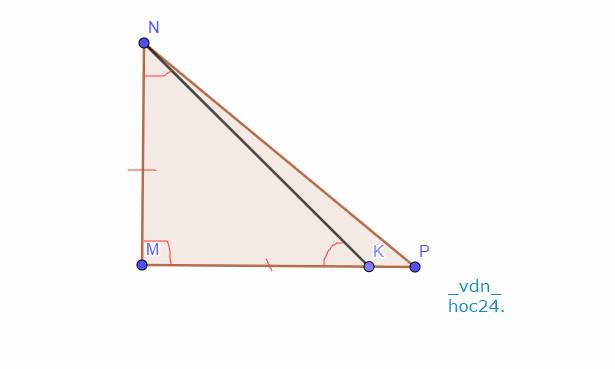
dạ thưa anh/chị em mới học lớp 6