Tìm x biết [x+1,2]+[x+1,4]+[x+1,8]+[x+1,16]=1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
1
24 tháng 9 2017
Bấm máy tính F(x)570 VN Plus ta có
B = x(2x-y)-z(y-2x)
CALC : x= 1.2 y= 1,4 z= 1,8
Shif (=)
10 tháng 6 2018
(1,1 + 1,2 x 1,3 + 1,4 x 1,5 + 1,6 x 1,7 + 1,8 x 1,9) x (1,25 - 0,25 x 5)
= (1,1 + 1,2 x 1,3 + 1,4 x 1,5 + 1,6 x 1,7 + 1,8 x 1,9) x (1,25 - 1,25)
= (1,1 + 1,2 x 1,3 + 1,4 x 1,5 + 1,6 x 1,7 + 1,8 x 1,9) x 0
= 0
10 tháng 6 2018
ta thấy
0.25*5=1.25
vì 1.25-1.25=0
nên kết quả phép tính là 0
DN
1
TN
6 tháng 1 2017
\(\left(x+1,2\right)+\left(x+1,5\right)+...+\left(x+4,5\right)=61,18\)
\(\Leftrightarrow\left(x+x+...+x\right)+\left(1,2+1,5+...+4,5\right)=61,18\)
\(\Leftrightarrow12x+34,2=61,18\)
Số lẻ hình như sai đề
NT
2
21 tháng 9 2020
Ta có: \(\left|x+1,1\right|+\left|x+1,2\right|+\left|x+1,3\right|+\left|x+1,4\right|\ge0\left(\forall x\right)\)
=> \(5x\ge0\left(\forall x\right)\)
<=> \(x\ge0\left(\forall x\right)\)
Thay vào ta được:
\(x+1,1+x+1,2+x+1,3+x+1,4=5x\)
\(\Leftrightarrow4x+5=5x\)
\(\Rightarrow x=5\)
21 tháng 9 2020
Ta có: |x+1,1|\(\ge\)0
|x+1,2|\(\ge\)0
|x+1,3|\(\ge\)0
|x+1,4|\(\ge\)0
Suy ra: |x+1,1|+|x+1,2|+|x+1,3|+|x+1,4|\(\ge\)0
<=> 5x\(\ge\)0
=> x\(\ge\)0
Do đó: |x+1,1|+|x+1,2|+|x+1,3|+|x+1,4|=5x
<=> x+1,1+x+1,2+x+1,3+x+1,4=5x
4x+(1,1+1,2+1,3+1,4)=5x
4x+5 =5x
4x =5x-5
4x-5x =-5
(4-5)x =-5
-1x =-5
=> 1x =5
x =5:1
=> x =5
Vậy x cần tìm là 5
NA
3
6 tháng 12 2020
a) x*1,2+x*1,8=45
x*(1,2+1,8)=45
x*3=45
x=45:3
x=15
b)x*10,8-x*1,8=108
x*(10,8-1,8)=108
x*9=108
x=108:9
x=12
học tốt nha em ^_^
LM
Lê Minh Vũ
CTVHS
10 tháng 11 2021
\(a)\)\(x\times1,2+x\times1,8=45\)
\(\Rightarrow\)\(x\times\left(1,2+1,8\right)=45\)
\(\Rightarrow\)\(x\times3=45\)
\(\Rightarrow\)\(x=45\div3\)
\(\Rightarrow\)\(x=15\)
TP
8
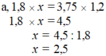
hình như đề sai với lại lớp 4 chưa học số thập phân