chứng minh với tam giác ABC có ba góc đều nhọn thì BC^2 = AB^2 + AC^2 - 2AB.ACcosA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 9 2023
Tham khảo:
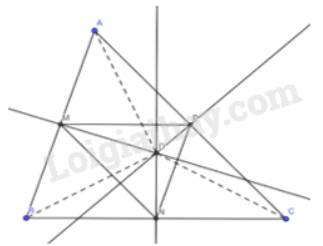
Theo giả thiết ta có :
OA = OB, MA = MB ( do M là trung điểm AB )
\( \Rightarrow \) MO là đường trung trực của đoạn thẳng AB
\( \Rightarrow \) MO vuông góc với AB
Theo giả thiết ta có :
OA = OC, PC = PA ( do P là trung điểm AC )
\( \Rightarrow \) PO là đường trung trực của đoạn thẳng AC
\( \Rightarrow \) PO vuông góc với AC
Theo giả thiết ta có :
OC = OB, NC = NB ( do N là trung điểm BC )
\( \Rightarrow \) NO là đường trung trực của đoạn thẳng BC
\( \Rightarrow \) NO vuông góc với BC
16 tháng 6 2023
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
góc BAD chung
=>ΔABD đồng dạng với ΔACE
b: ΔABD đồng dạng với ΔACE
=>AD/AE=AB/AC
=>AD/AB=AE/AC
=>ΔADE đồng dạng với ΔABC
16 tháng 6 2023
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng với ΔAEC
b: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
=>góc ADE=góc ABC
25 tháng 8 2023
a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
góc EAB chung
=>ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE/AB=AF/AC
Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc FAE chung
Do đó: ΔAEF đồng dạng với ΔABC
=>góc AEF=góc ABC
b: Kẻ HM//AB(M thuộc AC)
HN//AC(N thuộc AB)
Xét tứ giác AMHN có
AM//HN
AN//HM
Do đó: AMHN là hình bình hành
=>AM=HN; AN=HM
ΔAHM có AH<AM+MH
=>AH<AM+AN
HN//AC
mà BH vuông góc AC
nên HB vuông góc HN
ΔHBN vuông tại H
=>HB<BN
HM//AB
CH vuông góc AB
Do đó: HC vuông góc HM
=>ΔHCM vuông tại H
=>HC<MC
AH<AM+AN
HB<BN
HC<MC
=>HA+HB+HC<AM+AN+BN+MC=AC+AB
Chứng minh tương tự, ta được:
HA+HB+HC<AB+BC và HA+HB+HC<AC+BC
=>3*(HA+HB+HC)<2(BA+BC+AC)
=>HA+HB+HC<2/3*(BA+BC+AC)
9 tháng 10 2021
b: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔABH=ΔACK
11 tháng 2 2022
Xét ΔABC có BH<HC
mà AB là đường xiên của BH
và AC là đường xiên của CH
nên AB<AC