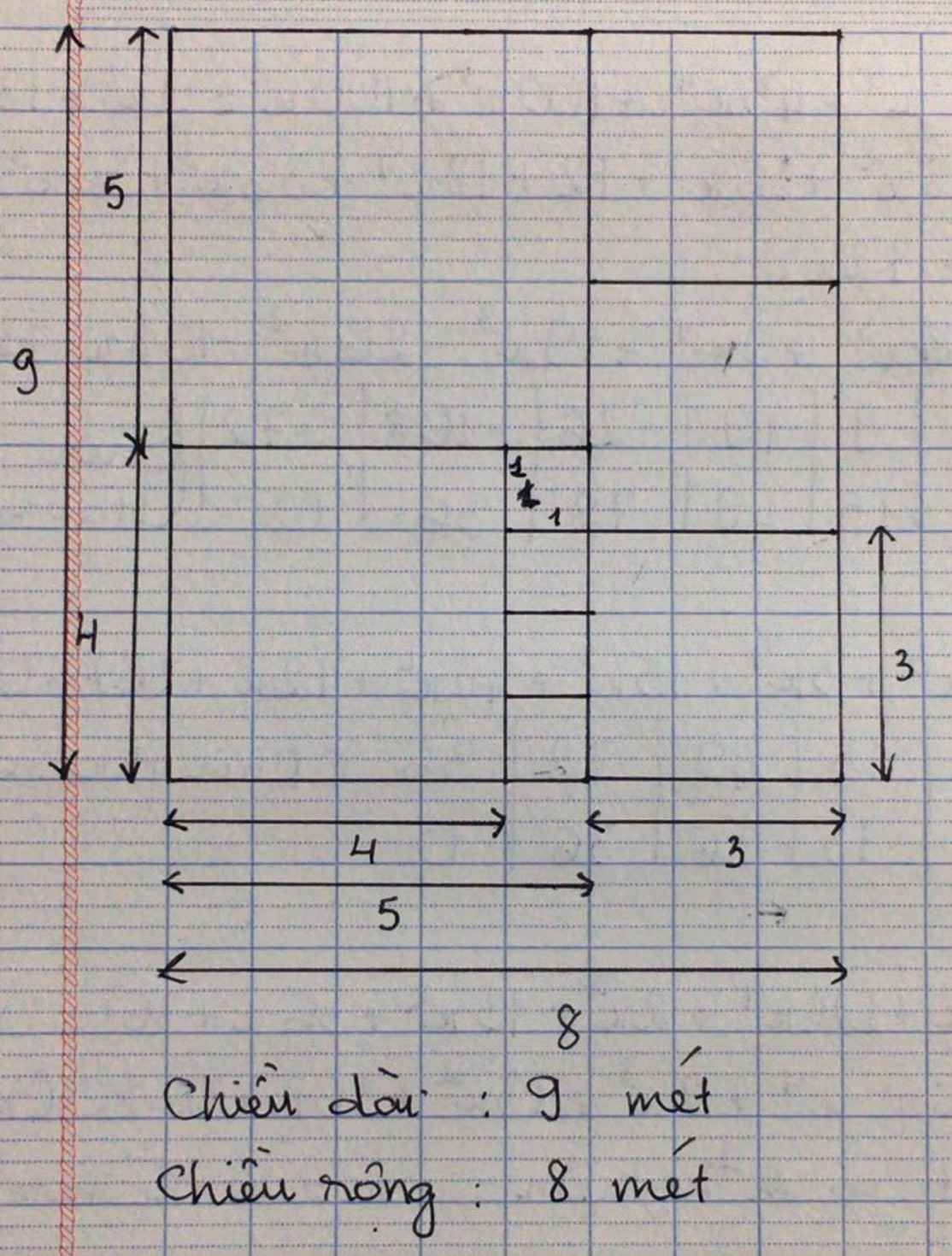
Khoảng đất được chia thành các ô vuông .Được biết kích thước của ao là 1 mét x 1 mét còn độ dài của tất cả của tất cả các cạnh của ô vuông là số nguyên. Hãy viết chiều dài và chiều rộng của toàn bộ khoảnh đất.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LM
26 tháng 4 2017
1) Tổng số phần là: 2 + 1 = 3 (phần)
Chiều dài là: 240 : 3 x 2 = 160 (m)
Chiều rộng là: 240 - 160 = 80 (m)
23 tháng 7 2023
a: Độ dài cạnh lớn nhất là ƯCLN(72;44)=4(m)
b: Số ô vuông chia được là:
72*44:4^2=198 ô
18 tháng 12 2019
Câu hỏi của Nguyễn Phương Thảo 2008 - Toán lớp 6 - Học toán với OnlineMath
T
12 tháng 11 2017
gọi a là cạnh của hình vuông. a(m) >0 a thuộc N
vì mảnh đát hình chữ nhật chia hết thành những ô vuông nên a là ước chung cảu 112.40 và a lớn nhất nên.
a là UWCLN (112,40)
giải tiếp nhé
11 tháng 1 2022
Gọi tích tất cả các số của mỗi hàng lần lượt là \(a_1,a_2,...,a_n\) và tương ứng số số bằng -1 ở mỗi hàng này lần lượt là \(m_1,m_2,...,m_n\). Khi đó \(a_i=\left(-1\right)^{m_i},\forall i\in\overline{1,n}\).
Tương tự gọi tích tất cả các số ở mỗi cột lần lượt là \(b_1,b_2,...,b_n\) và tương ứng số số bằng -1 ở mỗi cột này lần lượt là \(p_1,p_2,...,p_n\) thì \(b_i=\left(-1\right)^{p_i}.\forall i\in\overline{1,n}\).
Dễ thấy \(m_1+m_2+...+m_n=p_1+p_2+...+p_n\).
Giả sử tổng tất cả 2n tích đó bằng 0.
Khi đó \(\left(-1\right)^{m_1}+\left(-1\right)^{m_2}+...+\left(-1\right)^{m_n}+\left(-1\right)^{p_1}+\left(-1\right)^{p_2}+...+\left(-1\right)^{p_n}=0\).
Gọi x là số số chẵn trong các số \(m_1,m_2,...,m_n\) và y là số số chẵn trong số \(p_1,p_2,...,p_n\).
Ta có \(0=\left(-1\right)^{m_1}+\left(-1\right)^{m_2}+...+\left(-1\right)^{m_n}+\left(-1\right)^{p_1}+\left(-1\right)^{p_2}+...+\left(-1\right)^{p_n}=x-\left(n-x\right)+y-\left(n-y\right)=2\left(x+y\right)-2n\)
\(\Rightarrow x+y=n\).
Mà n lẻ nên x, y khác tính chẵn, lẻ.
Giả sử x chẵn, y lẻ. Khi đó \(m_1+m_2+...+m_n\) là số lẻ và \(p_1+p_2+...+p_n\) là số chẵn, vô lí.
Vậy...
12 tháng 7 2016
Độ dài lớn nhất của cạnh hình vuông chính là ƯCLN ( 52 ; 36)
Ta có:
52 = 22 . 13
36 = 22 . 32
Do đó ƯCLN ( 52 ; 36 ) = 22 = 4
Vậy cạnh hình vuông lớn nhất có độ dài là 4m.