K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DM
3
Những câu hỏi liên quan
26 tháng 3 2023
\(\text{#TNam}\)
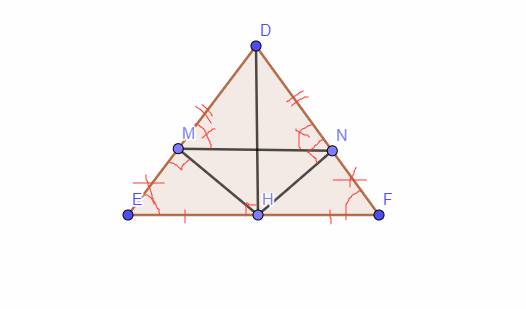
`a,` Xét Tam giác `HED` và Tam giác `HFD` có
`DE = DF (\text {Tam giác DEF cân tại D})`
\(\widehat{E}=\widehat{F}\) `(\text {Tam giác DEF cân tại D})`
`=> \text {Tam giác HED = Tam giác HDF (ch-gn)}`
`b,` Vì Tam giác `HED =` Tam giác `HFD (a)`
`-> HE = HF (\text {2 cạnh tương ứng})`
Xét Tam giác `HEM` và Tam giác `HFN` có:
`HE = HF (CMT)`
\(\widehat{E}=\widehat{F}\) `(a)`
\(\widehat{EMH}=\widehat{FNH}=90^0\)
`=> \text {Tam giác HEM = Tam giác HFN (ch-gn)}`
`-> EM = FN (\text {2 cạnh tương ứng})`
Ta có: \(\left\{{}\begin{matrix}DE=MD+ME\\DF=ND+NF\end{matrix}\right.\)
Mà `DE = DF, ME = NF`
`-> MD = ND`
Xét Tam giác `DMN: DM = DN (CMT)`
`-> \text {Tam giác DMN cân tại D}`
`->`\(\widehat{DMN}=\widehat{DNM}=\)\(\dfrac{180-\widehat{A}}{2}\)
Tam giác `DEF` cân tại `D`
`->`\(\widehat{E}=\widehat{F}=\)\(\dfrac{180-\widehat{A}}{2}\)
`->`\(\widehat{DMN}=\widehat{E}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {MN // EF (t/c 2 đt' //)}`
16 tháng 9 2023
a: Xét ΔADB và ΔADC có
AB=AC
góc BAD=góc CAD
AD chung
=>ΔADB=ΔADC
b: Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
góc EAD=góc FAD
=>ΔAED=ΔAFD
=>AE=AF và DE=DF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
7 tháng 3 2021
Xét ΔABC vuông tại A và ΔDEF vuông tại D có
BC=EF(gt)
AC=DF(gt)
Do đó: ΔABC=ΔDEF(cạnh huyền-cạnh góc vuông)
AH
Akai Haruma
Giáo viên
9 tháng 3 2021
Cách 1:
Xét tam giác $ABC$ và $DEF$ có:
$\widehat{A}=\widehat{D}=90^0$
$BC=EF$
$AC=DF$
$\Rightarrow \triangle ABC=\triangle DEF$ (ch-gcv)
Cách 2:
Vì $BC=EF; AC=DF\Rightarrow BC^2-AC^2=EF^2-DF^2$ hay $BA^2=ED^2$
$\Leftrightarrow BA=ED$ (theo định lý Pitago)
Hai tam giác $ABC$ và $DEF$ có các cạnh $AB=DE, BC=EF, AC=DF$ nên bằng nhau theo TH c.c.c
CM
9 tháng 3 2017
Theo kết quả câu a và câu b
MA + MB < IB + IA < CA + CB nên MA + MB < CA + CB.
chữ to dị, ai mà đọc đc, mờ quá
a) Xét \(\triangle BCH\) và \(\triangle BAH\) có:
BA = BC( \(\triangle ABC\) cân tại \(\hat{B}\) )
BH chung
\(\hat{A}=\hat{C}\) (\(\triangle ABC\) cân tại \(\hat{B}\) )
\(\Rightarrow\triangle BCH=\triangle BAH\left(c.c.c\right)\)
Nên \(\hat{BHA}=\hat{BHC};AH=HC\left(1\right)\)
Mà hai góc ở vị trí kề bù
\(\Rightarrow\hat{BAH}=\hat{BHC}=\frac{180^0}{2}=90^0\Rightarrow BH\bot AC\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\) BH là đường trung trực của AC
b) Do \(M\) là trung điểm \(B C\), và \(E\) là giao điểm của \(B H\) và đường vuông góc \(B C\) tại \(M\), suy ra \(E\) nằm trên đường trung trực của \(B C\).
Xét tam giác \(E A B\):
\(B H\) là đường cao trong tam giác cân \(A B C\), nên cũng là đường trung trực của \(A C\), do đó \(A E = E B\).
\(\Rightarrow\triangle EAB\) cân tại \(E\).
c) Do \(E\) nằm trên đường trung trực của \(B C\), nên \(E\) là trung điểm của đoạn \(B F\).
\(M\) là trung điểm của \(B C\) nên \(E F < B F\).
Vì \(D F = B F\), nên \(2 E F < D F\).