Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án: A
Để cường độ điện trường tại M bằng 0 thì hai vecto E 1 do q1 gây ra và E 2 do q2 gây ra phải ngược chiều và cùng độ lớn nên M nằm trên đường thẳng AB và ngoài đoạn AB
Do |q2| > |q1| nên r1 < r2 => r1 = r2 - AB,
=>
và r1 = 10 cm
Ta thấy \(\overrightarrow{E_1}=-4\overrightarrow{E_2}\) nên N nằm trong đoạn AB
Do đó nếu khoảng cách từ A tới N là r(m) thì khoảng cách từ B đến N là 0,5-r(m)
\(\overrightarrow{E_1}=-4\overrightarrow{E_2}\Rightarrow E_1=4E_2\Leftrightarrow k\cdot\dfrac{\left|q_1\right|}{r^2}=k\cdot\dfrac{\left|q_2\right|}{\left(0,5-r\right)^2}\)
\(\Leftrightarrow\dfrac{6.10^{-6}}{r^2}=4\cdot\dfrac{12.10^{-6}}{\left(0,5-r\right)^2}\)
\(\Leftrightarrow r\approx0,13\left(m\right)\)
\(\Rightarrow r=13\left(cm\right)\)
Chọn B
+ Vì q1 và q2 trái dấu nên q0 phải nằm ngoài đoạn thẳng nối AB.
+ Ta lại có: F 10 = F 20 ⇔ k q 1 q 0 AO 2 = k q 2 q 0 BO 2 ® AO = 3BO ® AO > BO ® q0 nằm ngoài và ở phía gần B hơn.
+ OA = AB + OB Û 3OB = 10 + OB ® OB = 5 cm
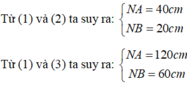
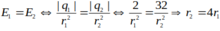
Đề bài:
Có hai điện tích điểm \(q_{1} = 2.1 \times 10^{- 9} \textrm{ } C\) và \(q_{2} = 8.1 \times 10^{- 6} \textrm{ } C\) đặt tại hai vị trí \(A\) và \(B\) cách nhau 9 cm trong chân không.
a) Tính cường độ điện trường tổng hợp do \(q_{1}\) và \(q_{2}\) gây ra tại điểm M là trung điểm của AB
\(E = \frac{k \cdot \mid q \mid}{r^{2}}\)
Trong đó:
\(E_{1} = \frac{k \cdot \mid q_{1} \mid}{r^{2}} = \frac{9 \times 10^{9} \times 2.1 \times 10^{- 9}}{\left(\right. 0.045 \left.\right)^{2}}\)
Tính giá trị:
\(E_{1} = \frac{9 \times 10^{9} \times 2.1 \times 10^{- 9}}{0.002025} = \frac{18.9}{0.002025} \approx 9333.33 \textrm{ } \text{N}/\text{C}\)
\(E_{2} = \frac{k \cdot \mid q_{2} \mid}{r^{2}} = \frac{9 \times 10^{9} \times 8.1 \times 10^{- 6}}{\left(\right. 0.045 \left.\right)^{2}}\)
Tính giá trị:
\(E_{2} = \frac{9 \times 10^{9} \times 8.1 \times 10^{- 6}}{0.002025} = \frac{73.29}{0.002025} \approx 36142.22 \textrm{ } \text{N}/\text{C}\)
\(E_{\text{t}ổ\text{ng}} = E_{2} - E_{1} = 36142.22 - 9333.33 \approx 26808.89 \textrm{ } \text{N}/\text{C}\)
b) Xác định vị trí điểm N tại đó cường độ điện trường tổng hợp do \(q_{1}\) và \(q_{2}\) gây ra bằng không
\(E_{1} = \frac{k \cdot \mid q_{1} \mid}{r_{1}^{2}}\)
\(E_{2} = \frac{k \cdot \mid q_{2} \mid}{r_{2}^{2}}\)
Để tổng cường độ điện trường bằng không, ta có phương trình:
\(E_{1} = E_{2}\) \(\frac{k \cdot \mid q_{1} \mid}{r_{1}^{2}} = \frac{k \cdot \mid q_{2} \mid}{r_{2}^{2}}\)
Rút gọn ta được:
\(\frac{\mid q_{1} \mid}{r_{1}^{2}} = \frac{\mid q_{2} \mid}{r_{2}^{2}}\) \(\frac{r_{2}^{2}}{r_{1}^{2}} = \frac{\mid q_{2} \mid}{\mid q_{1} \mid}\) \(\frac{r_{2}}{r_{1}} = \sqrt{\frac{\mid q_{2} \mid}{\mid q_{1} \mid}}\)
\(\frac{r_{2}}{r_{1}} = \sqrt{\frac{8.1 \times 10^{- 6}}{2.1 \times 10^{- 9}}} = \sqrt{\frac{8.1}{2.1}} = \sqrt{3.857} \approx 1.96\)
Vậy:
\(r_{2} = 1.96 \times r_{1}\)
\(r_{1} + 1.96 \times r_{1} = 9\) \(2.96 \times r_{1} = 9\) \(r_{1} = \frac{9}{2.96} \approx 3.04 \textrm{ } \text{cm}\)
Do đó:
\(r_{2} = 1.96 \times 3.04 \approx 5.96 \textrm{ } \text{cm}\)
Kết luận: