Bản chất định lý nhỏ Bézout (Định lý Bézout trong phép chia đa thức) là gì?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
28 tháng 10 2018
đặt \(f\left(x\right)=x^{2005}+x^{2004}\)
đa thức f(x) chia cho đa thức x - 1 có số dư là f(1) = 2
đa thức f(x) chia cho đa thức x + 1 có số dư là f(-1) = 0
đặt \(f\left(x\right)=\left(x^2-1\right).Q\left(x\right)+ax+b=\left(x-1\right)\left(x+1\right).Q\left(x\right)+ax+b\)
đẳng thức trên đúng với mọi x, nên thay lần lượt x = 1 và x = -1 ta được
\(\hept{\begin{cases}f\left(1\right)=0.2.Q\left(x\right)+a+b=2\\f\left(-1\right)=0\left(-2\right).Q\left(x\right)-a+b=0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}a+b=2\\b-a=0\end{cases}\Leftrightarrow\hept{\begin{cases}a=1\\b=1\end{cases}}}\)
vậy đa thức f(x) chia đa thức x2 - 1 có số dư là x + 1
VT
6 tháng 11 2017
Đáp án: B
Nguyên lý I của nhiệt động lực học: Độ biến thiên nội năng của hệ bằng tổng công và nhiệt lượng mà hệ nhận được: DU = Q + A
Q là nhiệt lượng trao đổi giữa hệ và môi trường: Q > 0 khi hệ nhận nhiệt, Q < 0 khi hệ tỏa nhiệt.
A là công do hệ thực hiện, A > 0 khi hệ nhận công, A < 0 khi hệ sinh công
Như vậy khi chất khí bị nén nhanh thì chất khí nhận công:
A > 0 → Q < 0 → chất khí nóng lên nhanh.
2 tháng 8 2021
Nhớ up tài liệu lên đây để mọi người cùng tải về nha admin VICE.
CM
28 tháng 10 2019
Ta có
Vì phần dư R = 0 nên Phép chia đa thức (2 x 3 – 26x – 24) cho đa thức x 2 + 4x + 3 là phép chia hết.
Do đó (I) đúng.
Lại có
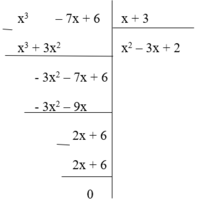
Nhận thấy phần dư R = 0 nên phép chia đa thức ( x 3 – 7x + 6) cho đa thức x + 3 là phép chia hết. Do đó (II) đúng
Đáp án cần chọn là: A
CM
8 tháng 11 2017
Lời giải
Ta có
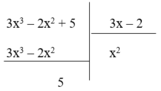
Vì phần dư R = 5 ≠ 0 nên phép chia đa thức 3 x 3 – 2 x 2 + 5 cho đa thức 3x – 2 là phép chia có dư. Do đó (I) sai
Lại có
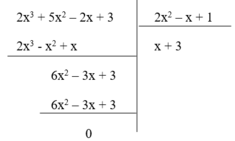
Nhận thấy phần dư R = 0 nên phép chia đa thức ( 2 x 3 + 5 x 2 – 2x + 3) cho đa thức (2 x 2 – x + 1) là phép chia hết. Do đó (II) đúng
Đáp án cần chọn là: D
20 tháng 11 2017
Gọi đa thức cần tìm là f(x); g(x),r(x), q(x) lần lượt là thương và số dư của f(x) cho x-2,x-3, x2-5x+6
Ta có f(x)= (x2-5x+6).2x+q(x)
Vì bậc của số dư luôn nhỏ hơn bậc của số bị chia mà x2-5x+6 có bậc là 2=> q(x) là đa thức bậc nhất => q(x)=ax+b
=> f(x)= (x2-5x+6).2x+ax+b=(x-2)(x-3).2x+ax+b
Ta cũng có
• f(x) = (x-2).g(x)+2
•f(x)= (x-3).r(x)+7
Ta xét các giá trị của x
+ x=2=> f(x)=2=> 2a+b=2(1)
+ x=3=> f(x) =7=> 3a+b= 7(2)
Lấy (2)-(1) ta có a=5=> b=-12
=> f(x)=(x2-5x+6).2x+5x-12
= 2x3-10x2+12x+5x-12= 2x3-10x2+17x-12
20 tháng 11 2017
các bạn làm cách nào cũng đc
ko bắt buộc phải dùng định lí bezout
Định lý Bézout (hay Định lý Bézout về các ước chung) là một kết quả quan trọng trong đại số và lý thuyết số, liên quan đến các đa thức và số nguyên.
Định lý Bézout cho rằng:
d(x)=u(x)f(x)+v(x)g(x)d(x)=u(x)f(x)+v(x)g(x)
ax+by=gcd(a,b)ax+by=gcd(a,b)
Đây là dạng cơ bản của định lý Bézout trong lý thuyết số. Định lý này được sử dụng rộng rãi trong việc tìm ước chung lớn nhất của hai số, giải quyết các phương trình Diophantine, và trong các ứng dụng mã hóa (như RSA).
Về bản chất, định lý Bézout cho phép ta biểu diễn ước chung lớn nhất của hai đa thức hoặc số nguyên dưới dạng một tổ hợp tuyến tính của chúng.