Cho đoạn thẳng AB. Trên cùng một nửa mặt phẳng có bờ là đường thẳng AB vẽ hai tia Ax, By lần lượt vuông góc với AB tại A, B. Gọi O là trung điểm của đoạn thẳng AB. Trên tia Ax lấy điểm C và trên tia By lấy điểm D sao cho \(\hat{COD}\) = \(90^{o}\) a. Gọi E là giao điểm của CO và BD. CMR: tam giác DCO = tam giác DOE từ đó suy ra AC+BD=CDb. Qua C kẻ đường thẳng song song với AB cắt OD tại H. CMR: EH...
Đọc tiếp
Cho đoạn thẳng AB. Trên cùng một nửa mặt phẳng có bờ là đường thẳng AB vẽ hai tia Ax, By lần lượt vuông góc với AB tại A, B. Gọi O là trung điểm của đoạn thẳng AB. Trên tia Ax lấy điểm C và trên tia By lấy điểm D sao cho \(\hat{COD}\) = \(90^{o}\)
a. Gọi E là giao điểm của CO và BD. CMR: tam giác DCO = tam giác DOE từ đó suy ra AC+BD=CD
b. Qua C kẻ đường thẳng song song với AB cắt OD tại H. CMR: EH vuông góc với CD
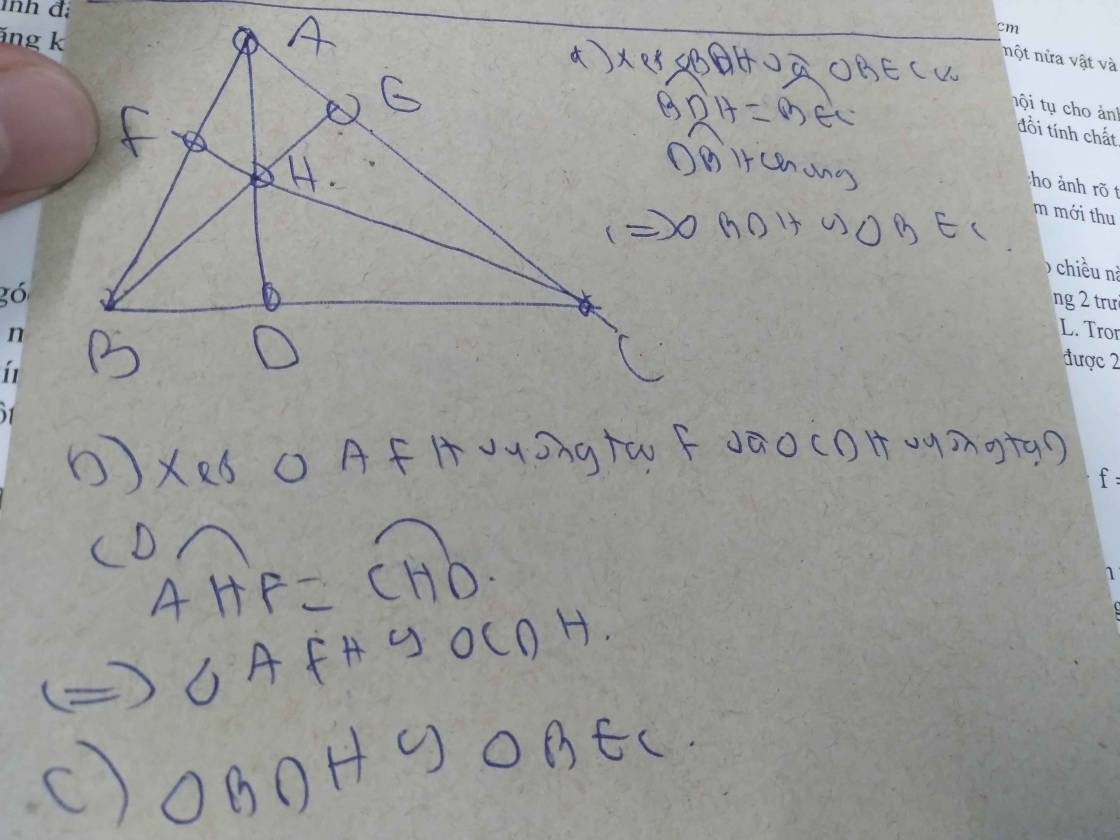
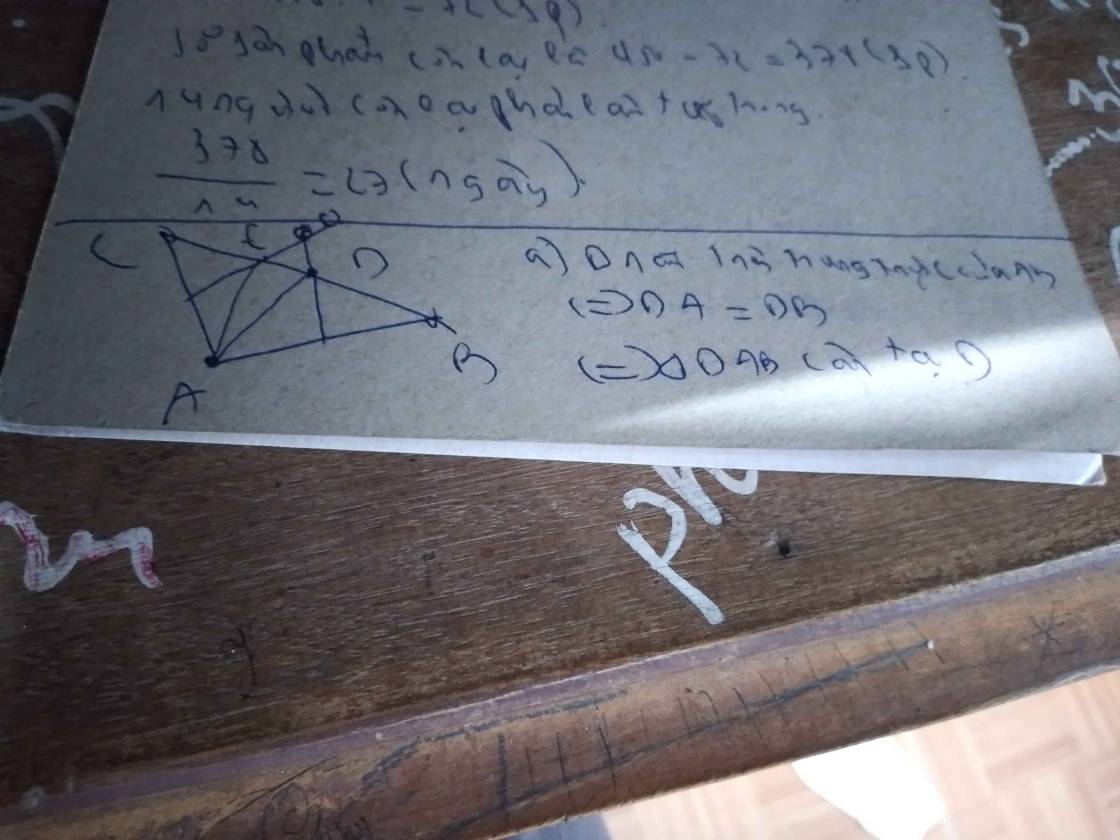
a: Xét ΔOAC vuông tại A và ΔOBE vuông tại B có
OA=OB
\(\widehat{AOC}=\widehat{BOE}\)(hai góc đối đỉnh)
Do đó: ΔOAC=ΔOBE
=>OC=OE và AC=BE
Xét ΔDOC vuông tại O và ΔDOE vuông tại O có
DO chung
OC=OE
Do đó: ΔDOC=ΔDOE
=>DC=DE
=>DC=DB+BE=DB+AC
b: Ta có: CH//AB
AB\(\perp\)BD
Do đó: CH\(\perp\)BD
Xét ΔCEH có
HO,ED là các đường cao
HO cắt ED tại D
Do đó: D là trực tâm của ΔCEH
=>CD\(\perp\)HE