Ví dụ 6: Cho tam giác ABC nhọn, kẻ 𝐴𝐻 ⊥ 𝐵𝐶 tại 𝐻, 𝐵𝐷 ⊥ 𝐴𝐶 tại 𝐷, 𝐶𝐸 ⊥ 𝐴𝐵 tại E. Chứng minh rằng a) 𝐴𝐻 < 1/2 (AB+AC) (𝐴𝐵 + 𝐴𝐶) b) 𝐴𝐻 + 𝐵𝐷 + 𝐶𝐸 < 𝐴𝐵 + 𝐵𝐶 + 𝐶A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 9 2017
Xét tam giác ABC vì BC là cạnh lớn nhất nên AB < BC và AC < BC.
Mà ta lại có: AC > 0 và AB > 0 hay 0 < AC và 0 < AB
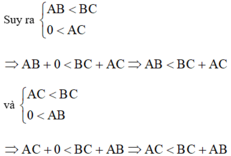
⇒ Đpcm
8 tháng 4 2015
a) ∆ABC có cạnh BC lớn nhất nên chân đường cao kẻ từ A phải nằm giữa B và C
=> HB + HC = BC
∆AHC vuông tại H => HC < AC
∆AHB vuông tại H => HB < AB
Cộng theo vế hai bất đẳng thức ta có:
HB + HC < AC + AB
Hay BC < AC + AB
b) BC là cạnh lớn nhất nên suy ra AB < BC và AC < BC
Do đó AB < BC + AC; AC < BC +AB
(cộng thêm AC hoặc AB vào vế phải của bất đẳng thức)
SC
27 tháng 3 2016
a) Xét tam giác vuông AHC có AC là cạnh lớn nhất ( cạnh lớn nhất trong tam giác vuông) => AC>HC (1) Xét tam giác vuông AHB có AB là cạnh lớn nhất (canh lớn nhất trong tam giác vuông) =>AB>HB (2) Ta có : HC+HB+BC ( H nằm giũa A và C) (3) Từ (1) , (2) và (3) => AC+AB>BC b)Xét tam giác ABC có BC là cạnh lớn nhất(gt) =>BC>AB Ta có : AC>0 => BC+AC>AB Xét tam giác ABC có BC là cạnh lớn nhất (gt) =>BC>AC Vì AB>0=>BC+AB>AC
CM
9 tháng 3 2017
Theo kết quả câu a và câu b
MA + MB < IB + IA < CA + CB nên MA + MB < CA + CB.
19 tháng 4 2017
a) ∆ABC có cạnh BC lớn nhất nên chân đường cao kẻ từ A phải nằm giữa B và C
=> HB + HC = BC
∆AHC vuông tại H => HC < AC
∆AHB vuông tại H => HB < AB
Cộng theo vế hai bất đẳng thức ta có:
HB + HC < AC + AB
Hay BC < AC + AB
b) BC là cạnh lớn nhất nên suy ra AB < BC và AC < BC
Do đó AB < BC + AC; AC < BC +AB
(cộng thêm AC hoặc AB vào vế phải của bất đẳng thức)
MT
1
7 tháng 3 2022
Thì bạn lấy một ví dụ đơn giản là A đi qua nhà B thì có hai cách là đi thẳng hoặc đi vòng. Nếu đi vòng thì độ dài quãng đường sẽ lớn hơn đi thẳng nên ta có bất đẳng thức tam giác
a: ΔAHB vuông tại H
=>AH<AB
ΔAHC vuông tại H
=>AH<AC
Ta có: AH<AB
AH<AC
Do đó: \(AH+AH< AB+AC\)
=>\(2AH< AB+AC\)
=>\(AH< \dfrac{1}{2}\left(AB+AC\right)\)
b: ΔDBC vuông tại D
=>BD<BC
ΔAEC vuông tại E
=>CE<CA
Ta có: AH<AB
BD<BC
CE<AC
Do đó: AH+BD+CE<AB+BC+AC