cho\((a+b+c)^2=a^2+b^2+c^2\) rút gọn \(p=\frac{a^2}{a^2+2bc}+\frac{b^2}{b^2+2ac}+\frac{c^2}{c^2+2ab}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 12 2017
a, \(\frac{2x+1}{2x^2-5x-3}\)
b, \(\frac{2x+1}{2x^2-5x-3}\)
\(=\frac{2x+1}{2x^2+x-6x-3}\)
\(=\frac{2x+1}{x\left(2x+1\right)-3\left(2x+1\right)}\)
\(=\frac{2x+1}{\left(2x+1\right)\left(x-3\right)}\)
\(=\frac{1}{x-3}\)
20 tháng 7 2016
bn hiu ve pt la dung roi va no rât qui để sau nay bn giải phuong trinh , con rut gọn la + - , : sao cho thu gọn đa thuc lai
vd 4x - 5 + x +9= 5x+ 4 vậy đó mk rút gọn xong
bn chu y nhieu đến pt vi nó quí lắm
KV
14 tháng 8 2023
a) √8/(√5 - √3)
= 2√2.(√5 + √3)/[(√5 - √3)(√5 + √3)]
= 2√2(√5 + √3)/2
= √10 + √6
b) √[(2 - √3)/(2 + √3)]
= √{(2 - √3)²/[(2 + √3)(2 - √3)]}
= (2 - √3)/(4 - 3)
= 2 - √3
AH
Akai Haruma
Giáo viên
14 tháng 8 2023
Lời giải:
a.
\(\frac{\sqrt{8}}{\sqrt{5}-\sqrt{3}}=\frac{\sqrt{8}(\sqrt{5}+\sqrt{3})}{(\sqrt{5}-\sqrt{3})(\sqrt{5}+\sqrt{3})}=\frac{\sqrt{8}(\sqrt{5}+\sqrt{3})}{5-3}=\sqrt{2}(\sqrt{5}+\sqrt{3})=\sqrt{10}+\sqrt{6}\)
b.
\(\sqrt{\frac{2-\sqrt{3}}{2+\sqrt{3}}}=\sqrt{\frac{(2-\sqrt{3})^2}{(2+\sqrt{3})(2-\sqrt{3})}}=\sqrt{\frac{(2-\sqrt{3})^2}{2^2-3}}=\sqrt{(2-\sqrt{3})^2}=|2-\sqrt{3}|=2-\sqrt{3}\)
PT
1
PT
1
PT
1
23 tháng 8 2021
\(\sqrt{\dfrac{3-\sqrt{5}}{3+\sqrt{5}}}=\sqrt{\dfrac{\left(3-\sqrt{5}\right)^2}{4}}=\dfrac{3-\sqrt{5}}{2}\)
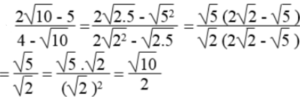
Ta có: \(\left(a+b+c\right)^2=a^2+b^2+c^2\)
=>\(a^2+b^2+c^2+2\left(ab+ac+bc\right)=a^2+b^2+c^2\)
=>2(ab+ac+bc)=0
=>2ab+2ac+2bc=0
=>ab+ac+bc=0
=>ab=-ac-bc; ac=-ab-bc; bc=-ab-ac
\(a^2+2bc=a^2+bc+bc=a^2+bc-ab-ac\)
\(=a^2-ab-ac+bc=a\left(a-b\right)-c\left(a-b\right)=\left(a-b\right)\left(a-c\right)\)
\(b^2+2ac=b^2+ac+ac=b^2+ac-ba-bc\)
\(=b^2-ba-bc+ac=b\left(b-a\right)-c\left(b-a\right)\)
=(b-c)(b-a)=-(a-b)(b-c)
\(c^2+2ab=c^2+ab+ab=c^2+ab-ac-bc\)
\(=c^2-ac-bc+ab=c\left(c-a\right)-b\left(c-a\right)=\left(c-a\right)\left(c-b\right)=\left(a-c\right)\left(b-c_{}\right)\)
\(P=\frac{2}{a^2+2bc}+\frac{2}{b^2+2ac}+\frac{2}{c^2+2ab}\)
\(=\frac{2}{\left(a-b\right)\left(a-c\right)}-\frac{2}{\left(a-b\right)\left(b-c\right)}+\frac{2}{\left(a-c\right)\cdot\left(b-c\right)}\)
\(=\frac{2\left(b-c\right)-2\left(a-c\right)+2\left(a-b\right)}{\left(a-b\right)\left(a-c\right)\left(b-c\right)}=\frac{2\left(b-c-a+c+a-b\right)}{\left(a-b\right)\left(a-c\right)\left(b-c\right)}=0\)