Question

[Thầy Cao Đô]

Cho hai đường tròn $(O;R)$ và $(O';r)$ tiếp xúc ngoài tại $A$ $\left(R>r \right)$. Gọi $BC$ là tiếp tuyến chung ngoài của hai đường tròn này (với $B \in (O)$ và $C\in (O')$). Tiếp tuyến chung tại $A$ của hai đường tròn $(O)$ và $(O')$ cắt đoạn thẳng $BC$ tại $M$.

a) Chứng minh $OM$ vuông góc với $O'M$.

b) Gọi $E$ là giao điểm của $AB$ với $OM$ và $F$ là giao điểm của $AC$ với $O'M$. Chứng minh $\widehat{MFE}=\widehat{EOO'}$.

c) Gọi $I$ là tâm đường tròn ngoại tiếp tứ giác $OEFO'$, $K$ là trung điểm của $AM$. Chứng minh $OO'=2IK.$

Answer 1

[Nguyễn Lê Phước Thịnh]

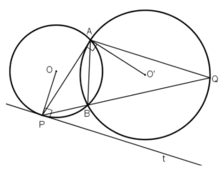
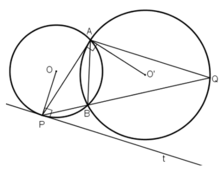
a: Xét (O) có

MA,MB là các tiếp tuyến

Do đó: MA=MB và MO là phân giác của góc AMB

Xét (O') có

MA,MC là các tiếp tuyến

Do đó: MA=MC và MO' là phân giác của góc AMC

MO là phân giác của góc AMB

=>\(\widehat{AMB}=2\cdot\widehat{AMO}\)

MO' là phân giác của góc AMC

=>\(\widehat{AMC}=2\cdot\widehat{AMO'}\)

Ta có: \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)

=>\(2\left(\widehat{AMO}+\widehat{AMO'}\right)=180^0\)

=>\(2\cdot\widehat{OMO'}=180^0\)

=>\(\widehat{OMO'}=90^0\)

=>MO\(\perp\)MO'

b: Ta có: MA=MC

=>M nằm trên đường trung trực của AC(1)

Ta có: OA=OC

=>O' nằm trên đường trung trực của AC(2)

Từ (1),(2) suy ra MO' là đường trung trực của AC

=>MO'\(\perp\)AC tại F

Ta có: MA=MB

=>M nằm trên đường trung trực của AB(3)

Ta có: OA=OB

=>O nằm trên đường trung trực của AB(4)

Từ (3),(4) suy ra MO là đường trung trực của AB

=>MO\(\perp\)AB tại E

Xét ΔMAO vuông tại A có AE là đường cao

nên \(ME\cdot MO=MA^2\left(5\right)\)

Xét ΔMAO' vuông tại A có AF là đường cao

nên \(MF\cdot MO'=MA^2\left(6\right)\)

Từ (5),(6) suy ra \(ME\cdot MO=MF\cdot MO'\)

=>\(\dfrac{ME}{MO'}=\dfrac{MF}{MO}\)

Xét ΔMEF và ΔMO'O có

\(\dfrac{ME}{MO'}=\dfrac{MF}{MO};\widehat{EMF}\) chung

Do đó: ΔMEF~ΔMO'O

=>\(\widehat{MFE}=\widehat{EOO'}\)