\(\left(x-1\right)\left(x+1\right)\left(x+2\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
12 tháng 5 2021
Lời giải:
Đặt biểu thức trên là $A$ thì:
\(A=\frac{1}{x+1}:\frac{x^2+3x+2-2}{(x-1)(x+1)(x+2)}=\frac{1}{x+1}:\frac{x(x+3)}{(x-1)(x+1)(x+2)}\)
\(=\frac{1}{x+1}.\frac{(x-1)(x+1)(x+2)}{x(x+3)}=\frac{(x-1)(x+2)}{x(x+3)}\)
4 tháng 3 2022
\(\left(x-1\right)\left(-x+2\right)=0\Leftrightarrow x=1;x=2\)
\(\left(x+2\right)\left(x+1-x+3\right)=0\Leftrightarrow x=-2\)
\(\left(x-2\right)\left(x+3\right)-\left(x-2\right)\left(2x+5\right)=0\Leftrightarrow\left(x-2\right)\left(-x-2\right)=0\Leftrightarrow x=-2;x=2\)
4 tháng 3 2022
\(i,\left(x-1\right)\left(x+3\right)-\left(x-1\right)\left(2x+1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+3-2x-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(-x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\\ k,\left(x+2\right)\left(x+1\right)-\left(x-3\right)\left(x+2\right)=0\\ \Leftrightarrow\left(x+2\right)\left(x+1-x+3\right)=0\\ \Leftrightarrow4\left(x+2\right)=0\\ \Leftrightarrow x+2=0\\ \Leftrightarrow x=-2\\ l,\left(x-2\right)\left(x+3\right)=\left(x-2\right)\left(2x+5\right)\\ \Leftrightarrow\left(x-2\right)\left(2x+5\right)-\left(x-2\right)\left(x+3\right)=0\\ \Leftrightarrow\left(x-2\right)\left(2x+5-x-3\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
8 tháng 1 2022
\(1,2\left(x-3\right)+1=2\left(x+1\right)-9\\ \Rightarrow2x-6+1=2x+2-9\\ \Rightarrow2x-5=2x-7\\ \Rightarrow-2=0\left(vô.lí\right)\)
\(2,\dfrac{5-x}{2}=\dfrac{3x-4}{6}\\ \Rightarrow30-6x=6x-8\\ \Rightarrow12x=38\\ \Rightarrow x=\dfrac{19}{6}\)
\(3,\left(x-1\right)^2+\left(x+2\right)\left(x-2\right)=\left(2x+1\right)\left(x-3\right)\\ \Rightarrow x^2-2x+1+x^2-4=2x^2-6x+x-3\\ \Rightarrow2x^2-2x-3=2x^2-5x-3\\ \Rightarrow3x=0\\ \Rightarrow x=0\)
\(4,\left(x+5\right)\left(x-1\right)-\left(x+1\right)\left(x+2\right)=1\\ \Rightarrow x^2+5x-x-5-x^2-2x-x-2=1\\ \\ \Rightarrow x-7=1\\ \Rightarrow x=8\)
8 tháng 1 2022
\(5,\dfrac{6x-1}{15}-\dfrac{x}{5}=\dfrac{2x}{3}\\ \Rightarrow\dfrac{6x-1}{15}-\dfrac{3x}{15}=\dfrac{10x}{15}\\ \Rightarrow6x-1-3x=10x\\ \Rightarrow3x-1=10x\\ \Rightarrow7x=-1\\ \Rightarrow x=\dfrac{-1}{7}\)
\(6,\dfrac{5\left(x-2\right)}{2}-\dfrac{x+5}{3}=1-\dfrac{4\left(x-3\right)}{5}\\ \Rightarrow\dfrac{75\left(x-2\right)}{30}-\dfrac{10\left(x+5\right)}{30}=\dfrac{30}{30}-\dfrac{24\left(x-3\right)}{30}\\ \Rightarrow75\left(x-2\right)-10\left(x+5\right)=30-24\left(x-3\right)\\ \Rightarrow75x-150-10x-50=30-24x+72\\ \Rightarrow65x-200=102-24x\\ \Rightarrow89x=302\\ \Rightarrow x=\dfrac{320}{89}\)
25 tháng 7 2021
a/ \(x=\dfrac{-5}{12}\)
b/ \(x\approx-1,9526\)
c/ \(x=\dfrac{21-i\sqrt{199}}{10}\)
d/ \(x=\dfrac{-20}{13}\)
AH
Akai Haruma
Giáo viên
29 tháng 1 2023
Bạn nên tách bài ra để đăng. Không nên đăng 1 loạt như thế này.
29 tháng 1 2023
1: \(=\left(x^2+x\right)^2+3\left(x^2+x\right)+2-12\)
=(x^2+x)^2+3(x^2+x)-10
=(x^2+x+5)(x^2+x-2)
=(x^2+x+5)(x+2)(x-1)
2: \(=\left(x^2+5ax+4a^2\right)\left(x^2+5ax+6a^2\right)+a^4\)
\(=\left(x^2+5ax\right)^2+10a^2\left(x^2+5ax\right)+25a^2\)
\(=\left(x^2+5ax+5a^2\right)^2\)
3: \(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)\)
5: \(M=\left(n+1\right)\left(n^2+2n\right)+360\)
=n(n+1)(n+2)+360 chia hết cho 6
6A
7D
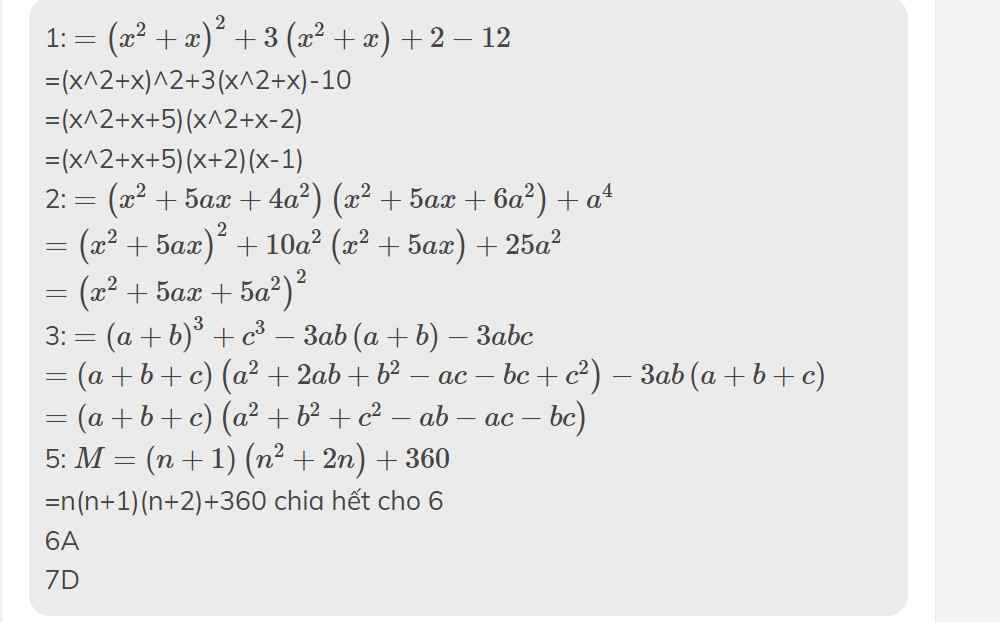
(x – 1)(x + 1)(x + 2) = ( x 2 + x – x – 1)(x + 2) = ( x 2 – 1)(x + 2) = x 2 ( x + 2) – 1.(x +2) = x 3 + 2 x 2 – x – 2
( x - 1 )( x + 1 )( x + 2 )=( \(x^2\) - 1 )( x + 2 )=\(x^3\) + 2\(x^2\) -x-2