Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có PQI = PIA ( cùng chắn PI) nên ΔAPI ~ΔAIQ(g.g）
=> AP/AI = AI/AQ =>Ap.AQ= AI^2 ( không đổi )
Giả sử đt ngoại tiếp tấm giác BPQ cắt AB tại D (D khác B)
Khi đó tam giác ADP ~ tam giác AQB =>AD/AQ = AP/AB
hay AD.AB = AP.AQ=AI^2 ( không đổi)
Do đó điểm D là điểm cố định (đpcm)
Suy ra : IA =IB (hai cung bằng nhau căng hai dây bằng nhau)
Hay I nằm trên đường trung trực của AB
Mà OA =OB (=R)
Nên O nằm trên đường trung trực của AB
Suy ra OI là đường trung trực của AB
Vì H là trung điểm của AB nên OI đi qua trung điểm H
Vậy ba điểm I, H, O thẳng hàng
Vì I là điểm chính giữa của cung AB nên IA=IB
=>I nằm trên đường trung trực của AB(1)
Ta có: HA=HB
nên H nằm trên đường trung trực của AB(2)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(3)
Từ (1), (2) và (3) suy ra O,H,I thẳng hàng
Đáp án A.
Trong các dây của đường tròn, dây lớn nhất là đường kính
Chọn đáp án A.
Trong các dây của đường tròn, dây lớn nhất là đường kính
Chọn đáp án A.
Trong các dây của đường tròn, dây lớn nhất là đường kính
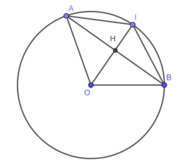
a. vì A; B ∈ (O) (1) nên OA = OB = R
=> △OAB là △ cân
lại có OH là đường cao (OH ⊥ AB)
=> OH cũng là đường phân giác
\(\rArr\hat{AOC}=\hat{BOC}\)
xét △OAC và △OBC, có:
OA = OB = R
\(\hat{AOC}=\hat{BOC}\) (cmt) (*)
OC là cạnh chung
=> △OAC = △OBC (c-g-c)
=> \(\hat{OAC}=\hat{OBC}=90^0\) (2)
Từ (1) (2) => BC là tiếp tuyến của đường tròn
b. ta có: AOB = AOC + BOC
mà AOC = BOC (từ *)
=> AOB = 2AOC = 2 x 60 = 120 độ
diện tích hình quạt AOB là:
\(S=\frac{\pi R^2n}{360}=\frac{\pi\cdot6^2\cdot120^0}{360^0}=12\pi\left(\operatorname{cm}^2\right)\)