Question

[0312_Nguyễn Minh Quân]

Cho tứ giác ABCD nội tiếp trong đường tròn (O; R). Vẽ tia Ax vuông góc với AD cắt BC tại E ; vẽ tia Ay vuông góc với AB cắt CD tại F. Chứng minh E,O,F thẳng hàng.

Answer 1

[Bùi Tường Vân]

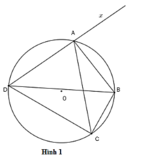
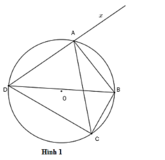
Để chứng minh ba điểm �E, �O, và �F thẳng hàng, ta sẽ sử dụng tính chất của tứ giác nội tiếp trong đường tròn và tính chất của các đường vuông góc.

Dữ kiện:

• Tứ giác ����ABCD nội tiếp trong đường tròn (�;�)(O;R).
• Tia ��Ax vuông góc với ��AD, cắt ��BC tại �E.
• Tia ��Ay vuông góc với ��AB, cắt ��CD tại �F.

Mục tiêu: Chứng minh rằng �E, �O, và �F thẳng hàng.

Bước 1: Xem xét các góc tạo thành bởi các đường vuông góc

• Vì ��Ax vuông góc với ��AD, ta có ∠���=90∘∠AxD=90∘.
• Tương tự, vì ��Ay vuông góc với ��AB, ta có ∠���=90∘∠AyB=90∘.

Bước 2: Tính chất của tứ giác nội tiếp

• Do tứ giác ����ABCD là tứ giác nội tiếp trong đường tròn, nên các góc ở các cặp đối diện của tứ giác này có tổng bằng 180∘180∘ (theo định lý góc đối diện trong tứ giác nội tiếp).

Cụ thể:

∠���+∠���=180∘vaˋ∠���+∠���=180∘∠ABC+∠ADC=180∘vaˋ∠BAD+∠BCD=180∘

Bước 3: Xem xét điểm �O, tâm của đường tròn

• Tâm �O là điểm giao của các đường vuông góc với các dây cung của đường tròn. Vì ����ABCD là tứ giác nội tiếp trong đường tròn, điểm �O có đặc tính quan trọng là nó nằm trên các đường vuông góc từ các điểm của tứ giác đến các cạnh đối diện của tứ giác.

Bước 4: Áp dụng lý thuyết giao tuyến của các đường vuông góc

• Vì �E là giao điểm của tia ��Ax vuông góc với ��AD và ��BC, và �F là giao điểm của tia ��Ay vuông góc với ��AB và ��CD, ta có thể chứng minh rằng các tia ��AE và ��AF sẽ đi qua một điểm chung — đó chính là điểm �O, điểm giao của các đường vuông góc trong đường tròn.

Bước 5: Kết luận

Do đó, ba điểm �E, �O, và �F thẳng hàng, vì chúng nằm trên các đường vuông góc từ các điểm của tứ giác nội tiếp đến các cạnh đối diện của nó, và điểm �O là điểm giao của các đường vuông góc này.

Như vậy, ta đã chứng minh được rằng �E, �O, và �F thẳng hàng.

Answer 2

[Nguyễn Bình]

chatgpt à BÙI TƯỜNG VÂN ?