Trong mặt phẳng tọa độ, tìm quĩ tích các điểm \(M\left(2m-1;m+3\right)\)với \(m\in R\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(AB=\sqrt{\left[2-\left(-2\right)\right]^2+\left(-1-2\right)^2}=5\)
\(BC=\sqrt{\left(5-2\right)^2+\left(3+1\right)^2}=5\)
Do đó: AB=BC
hay ΔABC cân tại B

a: \(AB=\sqrt{\left(2+2\right)^2+\left(-1-2\right)^2}=5\)
\(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
Do đó: ΔABC cân tại B

a: Thay x=0 và y=0 vào (d), ta được
\(2\cdot\left(m-1\right)\cdot0-\left(m^2-2m\right)=0\)
\(\Leftrightarrow m^2-2m=0\)
=>m=0 hoặc m=2
b: Khi m=3 thì (d): \(y=2\left(3-1\right)x-\left(3^2-2\cdot3\right)\)
\(\Rightarrow y=2\cdot2x-9+6=4x-3\)
Phương trình hoành độ giao điểm là:
\(x^2-4x+3=0\)
=>x=1 hoặc x=3
Khi x=1 thì y=1
Khi x=3 thì y=9

a: M(m;-2)
=>M nằm cùng lúc trên hai đường thẳng x=m trên đường thẳng y=-2
=>M là giao điểm của hai đường thẳng x=m và y=-2
b: M(5;m)
=>M nằm đồng thời trên hai đường thẳng x=5 và đường thẳng y=m
=>M là giao điểm của hai đường thẳng x=5 và y=m
c: M(m-5;2m+3)
=>M sẽ nằm trên cùng lúc hai đường thẳng là x=m-5 và y=2m+3
=>M là giao điểm của hai đường thẳng y=2m+3 và x=m-5

Đáp án A.
Ta có A M ⊥ B C ⊥ O A ⇒ B C ⊥ O A M ⇒ B C ⊥ O M
Tương tự ta cũng có O M ⊥ A C ⇒ O M ⊥ P ⇒ P (P) nhận O M ¯ = 3 ; 2 ; 1 là vecto pháp tuyến.
Trong các đáp án, chọn đáp án mặt phẳng có vecto pháp tuyến có cùng giá với O M ¯ và không chứa điểm M thì thỏa.

1, Ta có : y = mx - 2m - 1
<=> m ( x - 2 ) - 1 - y = 0
<=> m(x - 2) - (y+1) = 0
Dấu ''='' xảy ra khi x = 2 ; y = -1
Vậy (d) luôn đi qua A(2;-1)
2, (d) : y = mx - 2m - 1
Cho x = 0 => y = -2m - 1
=> d cắt Oy tại A(0;-2m-1)
=> OA = \(\left|-2m-1\right|\)
Cho y = 0 => x = \(\dfrac{2m+1}{m}\)
=> d cắt trục Ox tại B(2m+1/m;0)
=> OB = \(\left|\dfrac{2m+1}{m}\right|\)
Ta có : \(S_{OAB}=\dfrac{1}{2}\left|\dfrac{2m+1}{m}.\left(-2m-1\right)\right|=2\)
\(\Leftrightarrow\left|-\dfrac{\left(2m+1\right)^2}{m}\right|=4\Leftrightarrow\left[{}\begin{matrix}-\dfrac{\left(2m+1\right)^2}{m}=4\\-\dfrac{\left(2m+1\right)^2}{m}=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4m^2+8m+1=0\\4m^2+1=0\left(voli\right)\end{matrix}\right.\)
<=> m = \(\dfrac{-2\pm\sqrt{3}}{2}\)

Chọn A
Gọi A(a;0;0);B(0;b;0);C(0;0;c)
Phương trình mặt phẳng (P) có dạng:
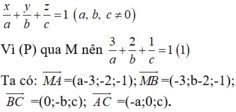
Vì M là trực tâm của tam giác ABC nên:
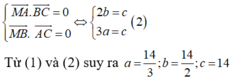
Khi đó phương trình (P): 3x+2y+z-14=0.
Vậy mặt phẳng song song với (P) là: 3x+2y+z+14=0.
