K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 11 2023
a: Sửa đề: A,B,M,O
Xét tứ giác BMOA có
\(\widehat{BMO}+\widehat{BAO}=90^0+90^0=180^0\)
=>BMOA là tứ giác nội tiếp
=>B,M,O,A cùng thuộc một đường tròn
b: Xét (O) có
BA,BM là tiếp tuyến
Do đó: BA=BM và OB là phân giác của \(\widehat{AOM}\)
=>\(\widehat{AOM}=2\cdot\widehat{AOB}\)
Xét (O) có
CA,CN là tiếp tuyến
Do đó: CA=CN và OC là phân giác của \(\widehat{AON}\)
=>\(\widehat{AON}=2\cdot\widehat{AOC}\)
\(\widehat{AON}+\widehat{AOM}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{AOC}+2\cdot\widehat{AOB}=180^0\)
=>\(2\cdot\widehat{BOC}=180^0\)
=>\(\widehat{BOC}=90^0\)
Xét ΔOBC vuông tại O có OA là đường cao
nên \(OA^2=AB\cdot AC\)
mà AB=BM và AC=CN
nên \(OA^2=BM\cdot CN\)
c: BA=BM
=>B nằm trên đường trung trực của AM(1)
OA=OM
=>O nằm trên đường trung trực của AM(2)
Từ (1) và (2) suy ra BO là đường trung trực của AM
=>BO\(\perp\)AM tại trung điểm của AM
=>BO\(\perp\)AM tại H và H là trung điểm của AM
CA=CN
=>C nằm trên đường trung trực của AN(3)
OA=ON
=>O nằm trên đường trung trực của AN(4)
Từ (3) và (4) suy ra CO là đường trung trực của AN
=>CO\(\perp\)AN tại trung điểm của AN
=>CO\(\perp\)AN tại K và K là trung điểm của AN
Xét tứ giác AHOK có \(\widehat{AHO}=\widehat{AKO}=\widehat{HOK}=90^0\)
nên AHOK là hình chữ nhật
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
8 tháng 5 2021
Ta có
DB=DM; EC=EM; AB=AC (2 tiếp tuyến cùng xp từ 1 điểm ngoài đường tròn thì khoảng cách từ điểm đó đến các tiếp điểm = nhau)
\(C_{ADE}=AD+DM+AE+EM=AD+DB+AE+EC=\)
\(=AB+AC=2AB\)
16 tháng 4 2021
Bạn tự vẽ hình nha!
c) Các tam giác ACM và BDM cân tại C và D; CO là phân giác góc ACM; DO là phân giác góc BDM => Các đường phân giác này cũng là đường cao => CO vuông góc với AM tại E và DO vuông góc với BM tại F => g. OEM = OFM = 90o.
Mặt khác g.AMB =90o(Góc nội tiếp chắn nửa đường tròn) => Từ giác OEMF là hình chữ nhật => I là trung điểm của OM => IO = OM/2 = R/2 (Không đổi)
Do đó khi M di chuyển thì trung điểm I của EF luôn cách O một khoảng không đổi R/2 => Quỹ tích trung điểm I của EF là nửa đường tròn tâm O bán kính R/2 cùng phía với nửa đường trón tâm O đường kính AB.
27 tháng 10 2023
a: ΔOAB cân tại O
mà OC là đường cao
nên OC là phân giác của \(\widehat{AOB}\)
Xét ΔOAC và ΔOBC có
OA=OB
\(\widehat{AOC}=\widehat{BOC}\)
OC chung
Do đó: ΔOAC=ΔOBC
=>\(\widehat{OAC}=\widehat{OBC}=90^0\)
=>CB là tiếp tuyến của (O)
b: Gọi giao điểm của AB với OC là H
ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
=>HA=HB=12(cm)
ΔAHO vuông tại H
=>\(HA^2+HO^2=AO^2\)
=>\(HO^2=15^2-12^2=81\)
=>HO=9(cm)
Xét ΔOAC vuông tại A có AH là đường cao
nên OH*OC=OA^2
=>OC=15^2/9=25(cm)
6 tháng 5 2021
\(=\sqrt{64}=8\left(cm\right)\)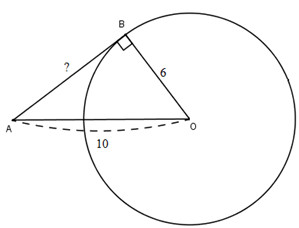
Áp dụng định lý Pytago vào tam giác AOB vuông tại B, ta có:
AB=\(\sqrt{AO^2-OB^2}=\sqrt{10^2-6^2}\)\(=\sqrt{64}=8\left(cm\right)\)
a: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2=R^2\)
b: ΔODE cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)DE tại I
Xét ΔFOA có
AI,OB là các đường cao
AI cắt OB tại G
Do đó: G là trực tâm của ΔFOA
=>FG\(\perp\)OA
c: Gọi H là trung điểm của FA
ΔFIA vuông tại I
mà IH là đường trung tuyến
nên IH=HA=HF
=>H là tâm đường tròn ngoại tiếp ΔFIA
ΔOIG vuông tại I
mà IQ là đường trung tuyến
nên QI=QG
=>ΔQIG cân tại Q
\(\widehat{HIQ}=\widehat{HIG}+\widehat{QIG}=\widehat{HAI}+\widehat{QGI}\)
mà \(\widehat{QGI}=\widehat{BGA}\)(hai góc đối đỉnh)
nên \(\widehat{HIQ}=\widehat{BGA}+\widehat{BAG}=90^0\)
=>HI\(\perp\)IQ
=>IQ là tiếp tuyến của đường tròn ngoại tiếp ΔFIA