Tính Tổng: S = 1 + 1/2+1/4+1/8+1/16
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
24 tháng 6 2017
Cộng thêm 1/2 vào biểu thức đã cho, có:
S + 1/2= 1/2+1/4+ 1/8+ 1/16+1/32+1/64+1/128
Nhận xét:
TT
1
12 tháng 3 2018
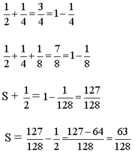
BÀI 1:
\(S=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\)
\(S=1+\frac{1}{1.2}+\frac{1}{2.2}+\frac{1}{2.4}+\frac{1}{4.4}+\frac{1}{4.8}\)
\(S=1+1-\frac{1}{2}+\frac{1}{2}-\frac{1}{2}+\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{4}+\frac{1}{4}-\frac{1}{8}\)
\(S=1+1-\frac{1}{8}\)
\(S=\frac{15}{8}\)
BÀI 2:
\(A=1.2+2.3+3.4+...+98.99\)
\(\Rightarrow3A=1.2.3+2.3.3+3.4.3+...+98.99.3\)
\(3A=1.2.\left(3-0\right)+2.3.\left(4-1\right)+3.4.\left(5-2\right)+...+98.99.\left(100-97\right)\)
\(3A=1.2.3+2.3.4-1.2.3+3.4.5-2.3.4+...+98.99.100-97.98.99\)
\(3A=\left(1.2.3+2.3.4+3.4.5+98.99.100\right)-\left(1.2.3+2.3.4+...+97.98.99\right)\)
\(3A=98.99.100\)
\(3A=970200\)
\(\Rightarrow A=970200:3\)
\(A=323400\)
CHÚC BN HỌC TỐT!!!
22 tháng 10 2016
S=1/2+1/4+1/8+1/16+1/32+1/64
S=1-1/2+1/2-1/4+1/4-1/8+1/8-1/16+1/16-1/32+1/32-1/64
S=1-1/64
S=63/64
TN
6
TN
2
KB
23 tháng 6 2015
S = 1 + 2 + 2x2 + 2x2x2 + ... +2x2x..x2 (13 thừ sô nhân 2)
2S = 2 + 2x2 +2x2x2 +..+2x2x2x..x2 (14 thùa số)
2S - S = 2 + 2x 2 + 2x 2x 2 + .. +2x2x2..x2(14 số x2 ) - 1 - 2 - 2x2 - 2x 2 - ... - 2x2x2..x2 ( 13 thừa số nhân 2)
S = 2x2x2x..x2 (14 thừa số) - 1
S = 16384 - 1 = 16383
Chúc bạn học tốt....
HT
6 tháng 6 2017
Sx2=[1+2+4+8+16+32+...+8192]x2
sx2=[2+4+8+16+32+64+...16384]
sx2-s=(2+4+8+16+32+64+...16384)-(1+2+4+8+16+32+...+8192)
s=16384-1
s=16383
16 tháng 4 2023
Ta có S = \(\dfrac{1}{2}+\dfrac{2}{4}+\dfrac{3}{8}+\dfrac{4}{16}+...+\dfrac{10}{2^{10}}\)
= \(\dfrac{1}{2}+\dfrac{2}{2^2}+\dfrac{3}{2^3}+\dfrac{4}{2^4}+...+\dfrac{10}{2^{10}}\)
2S = 1 + \(\dfrac{2}{2}+\dfrac{3}{2^2}+\dfrac{4}{2^3}+...+\dfrac{10}{2^9}\)
2S - S = ( 1 + \(\dfrac{2}{2}+\dfrac{3}{2^2}+\dfrac{4}{2^3}+...+\dfrac{10}{2^9}\)) - ( \(\dfrac{1}{2}+\dfrac{2}{2^2}+\dfrac{3}{2^3}+\dfrac{4}{2^4}+...+\dfrac{10}{2^{10}}\))
S = 1 + \(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^9}-\dfrac{10}{2^{10}}\)
Đặt A = 1 + \(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^9}\)
2A = 2 + 1 + \(\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^8}\)
2A - A = ( 2 + 1 + \(\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^8}\)) - ( 1 + \(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^9}\))
A = 2 - \(\dfrac{1}{2^9}\)
⇒ S = 2 - \(\dfrac{1}{2^9}\) - \(\dfrac{10}{2^{10}}\) = \(\dfrac{2^{11}}{2^{10}}-\dfrac{2}{2^{10}}-\dfrac{10}{2^{10}}=\dfrac{2^2\left(2^9-3\right)}{2^{10}}=\dfrac{2^9-3}{2^8}\)
Vậy S = \(\dfrac{2^9-3}{2^8}\)
LT
0
\(S=1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}\)
\(=1+\dfrac{8}{16}+\dfrac{4}{16}+\dfrac{2}{16}+\dfrac{1}{16}\)
\(=1+\dfrac{15}{16}=\dfrac{31}{16}\)
\(\dfrac{31}{16}\) nha bạn