A=\(\dfrac{\sqrt{x+1}}{\sqrt{x-2}}\)
cứu mai thi rồi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 9 2021
g: \(\dfrac{\sqrt{x}+3}{x\sqrt{x}+27}=\dfrac{1}{x-3\sqrt{x}+9}\)
h: \(\dfrac{2x-2\sqrt{x}+2}{x\sqrt{x}+1}=\dfrac{2}{\sqrt{x}+1}\)
i: \(\dfrac{x-3\sqrt{x}+2}{x-\sqrt{x}}=\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
k: \(\dfrac{x+7\sqrt{x}+12}{x-9}=\dfrac{\sqrt{x}+4}{\sqrt{x}-3}\)
i: \(\dfrac{x+\sqrt{x}-2}{x-2\sqrt{x}+1}=\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\)
18 tháng 8 2021
a: Ta có: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{3\sqrt{x}+1}{x-1}\)
\(=\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}+1-3\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{2x-3\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\left(2\sqrt{x}-1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\)
18 tháng 8 2021
b: Ta có: \(\left(\sqrt{x}+1\right)\cdot A=x\)
\(\Leftrightarrow\left(\sqrt{x}+1\right)\cdot\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}=x\)
\(\Leftrightarrow x-2\sqrt{x}+1=0\)
\(\Leftrightarrow x=1\left(loại\right)\)
4 tháng 9 2021
\(\dfrac{2x-2\sqrt{x}+2}{x\sqrt{x}+1}=\dfrac{2}{\sqrt{x}+1}\)
NU
28 tháng 8 2021
\(1,ĐKx\ge5\)
\(\sqrt{\left(x-5\right)\left(x+5\right)}+2\sqrt{x-5}=3\sqrt{x+5}+6\)
\(\Rightarrow\sqrt{x-5}\left(\sqrt{x+5}+2\right)-3\left(\sqrt{x+5}+2\right)=0\)
\(\Rightarrow\left(\sqrt{x+5}+2\right)\left(\sqrt{x-5}-3\right)=0\)
\(\left[{}\begin{matrix}\sqrt{x+5}=-2loại\\\sqrt{x-5}=3\end{matrix}\right.\)\(\Rightarrow x-5=9\Rightarrow x=14\)(TMĐK)
2a,ĐK \(x\ge0;x\ne9\)
,\(B=\dfrac{7\left(3-\sqrt{x}\right)-12}{\left(\sqrt{x}+1\right)\left(3-\sqrt{x}\right)}=\dfrac{9-7\sqrt{x}}{\left(\sqrt{x}+1\right)\left(3-\sqrt{x}\right)}\)
\(M=\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{9-7\sqrt{x}}{\left(\sqrt{x}+1\right)\left(3-\sqrt{x}\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}+\dfrac{9-7\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}=\dfrac{x-6\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}\)
\(M=\dfrac{\left(\sqrt{x}-3\right)^2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\)
9 tháng 11 2021
d: \(=-\left(x+\sqrt{x}-12\right)=-\left(\sqrt{x}+4\right)\left(\sqrt{x}-3\right)\)
TT
15 tháng 8 2020
Bài 2 :
b) \(\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}=2\) (1)
ĐKXĐ : \(x\ge1\)
Pt(1) tương đương :
\(\sqrt{\left(x-1\right)+2\sqrt{x-1}+1}+\sqrt{\left(x-1\right)-2\sqrt{x-1}+1}=2\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}+1\right)^2}+\sqrt{\left(\sqrt{x-1}-1\right)^2}=2\)
\(\Leftrightarrow\sqrt{x-1}+1+\left|\sqrt{x-1}-1\right|=2\) (*)
Xét \(x\ge2\Rightarrow\sqrt{x-1}-1\ge0\)
\(\Rightarrow\left|\sqrt{x-1}-1\right|=\sqrt{x-1}-1\)
Khi đó pt (*) trở thành :
\(\sqrt{x-1}+1+\sqrt{x-1}-1=2\)
\(\Leftrightarrow2\sqrt{x-1}=2\)
\(\Leftrightarrow\sqrt{x-1}=1\)
\(\Leftrightarrow x-1=1\)
\(\Leftrightarrow x=2\) ( Thỏa mãn )
Xét \(1\le x< 2\) thì \(x\ge2\Rightarrow\sqrt{x-1}-1< 0\)
Nên : \(\left|\sqrt{x-1}-1\right|=1-\sqrt{x-1}\). Khi đó pt (*) trở thành :
\(\sqrt{x-1}+1+1-\sqrt{x-1}=2\)
\(\Leftrightarrow2=2\) ( Luôn đúng )
Vậy tập nghiệm của phương trình đã cho là \(S=\left\{x|1\le x\le2\right\}\)
TT
15 tháng 8 2020
Bài 1 :
a) ĐKXĐ : \(-1\le a\le1\)
Ta có : \(Q=\left(\frac{3}{\sqrt{1+a}}+\sqrt{1-a}\right):\left(\frac{3}{\sqrt{1-a^2}}\right)\)
\(=\left(\frac{3+\sqrt{1-a}.\sqrt{1+a}}{\sqrt{1+a}}\right)\cdot\frac{\sqrt{1-a^2}}{3}\)
\(=\frac{3+\sqrt{\left(1-a\right)\left(1+a\right)}}{\sqrt{1+a}}\cdot\frac{\sqrt{\left(1-a\right)\left(1+a\right)}}{3}\)
\(=\frac{\left(3+\sqrt{1-a^2}\right).\sqrt{1-a}}{3}\)
Vậy \(Q=\frac{\left(3+\sqrt{1-a^2}\right).\sqrt{1-a}}{3}\) với \(-1\le a\le1\)
b) Với \(a=\frac{\sqrt{3}}{2}\) thỏa mãn ĐKXĐ \(-1\le a\le1\)nên ta có :
\(\hept{\begin{cases}1-a=1-\frac{\sqrt{3}}{2}=\frac{4-2\sqrt{3}}{4}=\frac{\left(\sqrt{3}-1\right)^2}{2^2}\\1-a^2=1-\frac{3}{4}=\frac{1}{4}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\sqrt{1-a}=\sqrt{\frac{\left(\sqrt{3}-1\right)^2}{2^2}}=\left|\frac{\sqrt{3}-1}{2}\right|=\frac{\sqrt{3}-1}{2}\\\sqrt{1-a^2}=\frac{1}{2}\end{cases}}\)
Do đó : \(Q=\frac{\left(3+\frac{1}{2}\right)\cdot\frac{\sqrt{3}-1}{2}}{3}=\frac{5\sqrt{3}-5}{12}\)
Y
11 tháng 4 2022
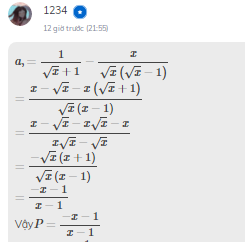
Mk ra đáp án khác với đáp án ủa bn nên bn bào sai chứ j, thật ra cả 2 đáp án đều giống nhau, do biến đổi dấu nên trở thành 2 đáp án khác nhau thôi :V
để mk lm lại phần đáp án của mk ra giống đáp án của bn nek :V
\(a,\)\(P=\dfrac{-x-1}{x-1}\)
\(\Rightarrow\dfrac{-\left(-x-1\right)}{-\left(x-1\right)}=\dfrac{x-1}{-x+1}=\dfrac{x-1}{1-x}\)
Còn câu b thì hôm qua bn ghi là \(x=\dfrac{1}{\sqrt{2}}\) chứ có pk là \(1\sqrt{2}\) đou >:V
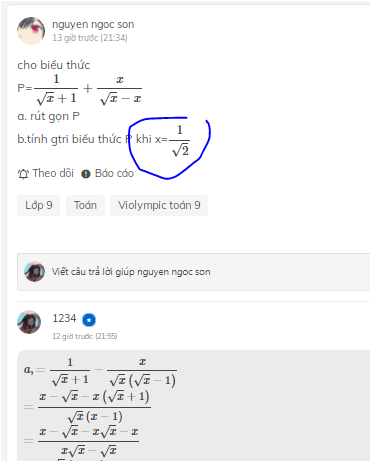
\(b,\)Thay \(x=1\sqrt{2}\) vào \(P\) ta có :
\(P=\dfrac{x-1}{1-x}\)
\(P=\dfrac{1\sqrt{2}-1}{1-1\sqrt{2}}=3+2\sqrt{2}\)
ông học trường nào lớp mấy vậy