c1: A
C2: B
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B.
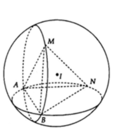
Trên hai đường tròn ( C 1 ) , ( C 2 ) lần lượt lấy M, N sao cho hai điểm này không trùng hai điểm A, B. Khi đó 4 điểm M, N, A, B không đồng phẳng nên tạo thành tứ diện ABMN. Mặt cầu ( S ) đi qua ( C 1 ) , ( C 2 ) khi đó mặt (S) đi qua A, B, M, N
Do đó có duy nhất 1 mặt cầu

Đáp án B
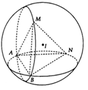
Trên hai đường tròn ( C 1 ) , ( C 2 ) lần lượt lấy M, N sao cho hai điểm này không trùng hai điểm A, B. Khi đó 4 điểm M, N, A, B không đồng phẳng nên tạo thành tứ diện ABMN. Mặt cầu (S) đi qua ( C 1 ) , ( C 2 ) khi đó mặt (S) đi qua A, B, M, N
Do đó có duy nhất 1 mặt cầu

\(f=\frac{1}{2\pi\sqrt{LC}}\)
khi mắc nối tiếp thì \(C=\frac{C_1C_2}{C_1+C_2}\)
khi mắc song song thì \(C'=C_1+C_2\)
Ta có \(\frac{f}{f'}=\sqrt{\frac{C'}{C}}=\frac{25}{12}\Rightarrow\frac{C}{C'}=\frac{625}{144}\)
\(\Leftrightarrow144\left(C_1+C_2\right)=625\frac{C_1C_2}{C_1+C_2}\)
\(\Leftrightarrow144C_1^2-337C_1C_2+144C^2_2=0\)
\(\Leftrightarrow\left(16C_1-9C_2\right)\left(9C_1-16C_2\right)=0\)
do \(C_1>C_2\Rightarrow C_1=\frac{16}{9}C_2\Leftrightarrow C_2=\frac{9}{16}C_1\)
Ta có \(f'=\frac{1}{2\pi\sqrt{L\left(C_1+C_2\right)}}=\frac{1}{2\pi\sqrt{LC_1\times\frac{25}{16}}}=24\)
\(\Rightarrow\frac{1}{2\pi\sqrt{LC_1}}\times\frac{4}{5}=24\Rightarrow\frac{1}{2\pi\sqrt{LC_1}}=30\)
hay f1=30 Hz CHỌN C
dòng thứ 4 trên xuống là \(\frac{C'}{C}=\frac{625}{144}\) nhé, mình viết nhầm đó ^^!

Đường tròn C 1 có tâm I 1 1 ; 2 và bán kính R 1 = 1 .
Đường tròn C 2 có tâm I 2 - 1 ; 0 và bán kính R 2 = 1 .

Chọn B
1A
2B
1:A 2:B