Nhân dịp mừng đảng, mừng xuân năm 2018, Hội người cao tuổi huyện Vĩnh Linh tổ chức giải cờ tướng đầu xuân. Theo danh sách đăng kí ban đầu có 128 cụ tham gia. sau ba vòng thi đấu loại trực tiếp, ban tổ chức giả đã lựa được 4 cụ có số điểm cao nhất vào vòng thi chung kết. Thể lệ hình thức thi đấu và cachs tính điểm như sau: Mỗi cụ phải thi 4 ván đấu. Nếu thắng 1 ván thì được 2 điểm còn nếu thua 1 ván thì bị trừ 2 điểm. nếu số điểm bị trừ bằng hoặc lớn hơn số điểm đạt được thì coi nhơ là 0 điểm. trong vòng chung kết nầy chắc chắn có ít nhất 2 cụ có cùng số điểm. Em hãy giải thích điều đó?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: A là tập hợp 32 đội tham gia World Cup 2018.
B là tập hợp 16 đội sau vòng thi đấu bảng (chọn từ 32 đội của tập hợp A sau thi thi đấu theo bảng)
Rõ ràng mỗi phần tử (mỗi đội) của tập hợp B cũng là một phần tử (một đội) của tập hợp A.
Do đó: \(B \subset A\)
Tương tự: Từ 16 đội của B, sau khi đấu loại trực tiếp, còn lại 8 đội vào tứ kết kí hiệu là tập hợp C
Do đó: \(C \subset B\)
Vậy \(C \subset B \subset A\).
b) Tập hợp \(A \cap C\) gồm các đội bóng vừa thuộc 32 đội tham gia World Cup 2018, vừa thuộc 8 đội thi đấu vòng tứ kết, chính là 8 đội của tập hợp C.
Tập hợp \(B \cap C\) gồm các đội bóng vừa thuộc 16 đội sau vòng thi đấu bảng, vừa thuộc 8 đội thi đấu vòng tứ kết, chính là 8 đội của tập hợp C.
Vậy \(A \cap C = B \cap C = C\)
c) Tập hợp \(A\,{\rm{\backslash }}\,B\) gồm các đội thuộc 32 đội tham gia World Cup 2018 nhưng không thuộc 16 đội sau vòng thi đấu bảng.
Vậy đó là 16 đội không vượt qua vòng thi đấu bảng.
Nói cách khác: Tập hợp \(A\,{\rm{\backslash }}\,B\) gồm các đội bóng bị loại sau vòng đấu bảng.

thì bạn cứ chia ra thành nhieuf trận đến khi hết
14 : 2 = 7 ( 1 trận )
7 : 2 = 3 dư 1 ( 2 trận )
( 3 + 1 ) : 2 = 2 ( 3 trận )
2 : 2 = 1 ( 4 trận )
Vậy kết luận phải đấu 4 trận mới xong

Chọn A
+ Chia đều 10 đội vào 2 bảng A và B có ![]() cách.
cách.
Do đó số phần tử của không gian mẫu là : ![]()
+ Sắp xếp đội của lớp 10A1 và 10A2 vào 2 bảng khác nhau A và B có 2! cách.
Chọn 4 đội trong 8 đội còn lại để xếp vào bảng có đội lớp 10A1 có C 8 4 cách.
Bốn đội còn lại xếp vào bảng còn lại.
Suy ra số cách chia đều 10 đội vào 2 bảng sao cho 2 đội 10A1 và 10A2 nằm ở 2 bảng khác nhau là ![]()
Gọi A là biến cố “Chia đều 10 đội vào 2 bảng sao cho 2 đội 10A1 và 10A2 nằm ở 2 bảng khác nhau ” thì số các kết quả thuận lợi cho biến cố A là: ![]()
+ Xác suất cần tìm là: 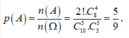


Mỗi trận bóng đá gồm 2 đội lấy từ 12 đội Vậy số trận diễn ra từ 12 đội coi như là số tổ hợp chập 2 của 12 phần tử , vậy có C212C122=66 trận.
- vì có lượt đi và lượt về nên số trận đấu là 66.2=132 trận.

Chọn C
+ Chia đều 16 đội vào 4 bảng có ![]()
+ Sắp xếp 3 đội của 3 lớp Toán vào 3 bảng khác nhau trong 4 bảng có A 4 3 cách.
Chọn 3 đội trong 13 đội còn lại để xếp vào bảng có đội lớp 10 Toán có C 13 3 cách.
Chọn 3 đội trong 10 đội còn lại để xếp vào bảng có đội lớp 11 Toán có C 10 3 cách.
Chọn 3 đội trong 7 đội còn lại để xếp vào bảng có đội lớp 12 Toán có C 7 3 cách.
Bốn đội còn lại xếp vào bảng còn lại.
Suy ra số cách chia đều 16 đội vào 4 bảng sao cho 3 đội của 3 lớp Toán nằm ở 3 bảng khác nhau là ![]()
+ Xác suất cần tìm là: