Câu 15. (1,0 điểm). Bác Phương chia số tiền $800$ triệu đồng của mình cho hai khoản đầu tư. Sau một năm, tổng số tiền lãi bác thu được là $54$ triệu đồng. Lãi suất cho khoản đầu tư thứ nhất là $6\%$/năm và khoản đầu tư thứ hai là $8\%$/năm. Tính số tiền bác Phương đầu tư cho mỗi khoản.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tổng số vốn của 3 bác Xuân, Yến, Dũng là : 300 + 400 + 500 = 1200 triệu đồng .
Tỉ lệ vốn của bác Xuân là : \(\dfrac{{300}}{{1200}}\)\( = \dfrac{1}{4}\)
TỈ lệ góp vốn của bác Yến là : \(\dfrac{{400}}{{1200}}\)\( = \dfrac{1}{3}\)
Tỉ lệ góp vốn của bác Dũng là : \(\dfrac{{500}}{{1200}}\) \( = \dfrac{5}{{12}}\)
Từ các tỉ lệ góp vốn trên ta tính được tỉ lệ lãi của mỗi người theo số vốn là :
Bác Xuân có số lãi là : \(\dfrac{1}{4} \times 240\)= 60 ( triệu đồng )
Bác Yến có số lãi là : \(\dfrac{1}{3} \times 240\)= 80 ( triệu đồng )
Bác Dũng có số lãi là : 240 – 80 - 60 = 100 ( triệu đồng )

a: y=150000000*(1+6,8%)*x=160200000x
b: Sau 5 năm số tiền nhận được là:
160200000*5=801000000(đồng)

Đáp án B
Gọi A là số tiền gốc ban đầu, lãi suất r/năm, số tiền gửi thêm là a (triệu đồng)
Sau năm đầu tiên, số tiền cả gốc lẫn lãi mà ông Minh nhận đc là A(1+r)
Sau năm thứ 2, cả gốc và lãi ông nhận được là
![]()
Sau năm thứ 3, cả gốc và lãi ông nhận được:
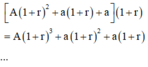
Sau năm thứ n, ông Minh nhận được số tiền:
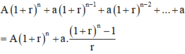
Thay số: sau 10 năm ông Minh nhận về cả gốc lẫn lãi là
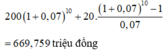
Đáp án B
Gọi A là số tiền gốc ban đầu, lãi suất r/năm, số tiền gửi thêm là a (triệu đồng)
Sau năm đầu tiên, số tiền cả gốc lẫn lãi mà ông Minh nhận đc là A(1+r)
Sau năm thứ 2, cả gốc và lãi ông nhận được là
![]()
Sau năm thứ 3, cả gốc và lãi ông nhận được:
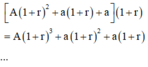
Sau năm thứ n, ông Minh nhận được số tiền:
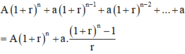
Thay số: sau 10 năm ông Minh nhận về cả gốc lẫn lãi là
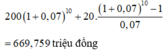

Đáp án C
Gọi A là số tiền gốc ban đầu, lãi suất r / năm, số tiền gửi thêm là a (triệu đồng).
Sau năm đầu tiên, số tiền cả gốc lẫn lãi mà ông Minh nhận được là: A 1 + r
Sau năm thứ 2, cả gốc và lãi ông nhận được là: A 1 + r + a 1 + r = A 1 + r 2 + a 1 + r
Sau năm thứ 3, cả gốc và lãi ông nhận được:
A 1 + r 2 + a 1 + r + a 1 + r = A 1 + r 3 + a 1 + r 2 + a 1 + r
…
Sau năm thứ n, ông Minh nhận được số tiền:
A 1 + r n + a 1 + r n − 1 + a 1 + r n − 2 + . .. + a = A 1 + r n + a . 1 + r n − 1 r
Thay số: sau 10 năm ông Minh nhận về cả gốc lẫn lãi là
200 1 + 0 , 07 10 + 20. 1 + 0 , 07 10 − 1 0 , 07 = 669 , 759 triệu đồng.

Gọi số tiền ban đầu của chi Ba là x(đồng)là số tiền chị Ba có lúc ban đầu(xϵN✳)
thì:số tiền chị Ba đầu tư vào quán cà phê là:\(\dfrac{x}{2}\)
số tiền chị Ba nhận được là\(\dfrac{x}{2}+10\%.\dfrac{x}{2}\)
số tiền chị Ba đầu tư vào quán ăn là:\(\dfrac{x}{4}\)
số tiền chị Ba nhân được:\(\dfrac{x}{4}+12\%.\dfrac{x}{4}\)
số tiền chị Ba còn lại sau khi đầu tư là:\(x-\dfrac{x}{2}-\dfrac{x}{4}\)
Ta có pt:\(x-\dfrac{x}{2}-\dfrac{x}{4}+10\%.\dfrac{x}{2}+12\%.\dfrac{x}{4}\)=192000000
⇔\(x-\dfrac{x}{2}-\dfrac{x}{4}+\dfrac{x}{20}+\dfrac{3x}{100}\)=192000000
⇔\(\dfrac{100x}{100}-\dfrac{50x}{100}-\dfrac{25x}{100}+\dfrac{5x}{100}+\dfrac{3x}{100}\)=\(\dfrac{19200000000}{100}\)
⇔\(\dfrac{100x-50x-25x+5x+3x}{100}=\dfrac{19200000000}{100}\)
⇔33x=19200000000
⇔x=5818181818(thỏa)
vậy số tiền ban đầu của chị Ba là 5818181818 đồng
⇔

Theo đề, ta có: A>=800
=>\(500\left(1+0.075\right)^n>=800\)
=>\(1.075^n>=1.6\)
=>\(n>=log_{1.075}1.6\simeq6.5\)
=>Sau ít nhất 7 năm thì số tiền bác Minh thu được là ít nhất 800 triệu

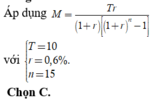
Gọi x (đồng) là số tiền khoản thứ nhất (x > 0)
Số tiền khoản thứ hai là: 800000000 - x (đồng)
Tổng số tiền lãi sau một năm bác Phương nhận được là:
0,06x + 0,08(800000000 - x) (đồng)
Theo đề bài, ta có phương trình:
0,06x + 0,08(800000000 - x) = 54000000
0,06x + 64000000 - 0,08x = 54000000
-0,02x = 54000000 - 64000000
-0,02x = -10000000
x = -10000000 : (-0,02)
x = 500000000 (nhận)
Vậy số tiền bác Phương đầu tư cho khoản thứ nhất là 500000000 đồng, số tiền bác Phương đầu tư cho khoản thứ hai là 800000000 - 500000000 = 300000000 đồng