K
Khách
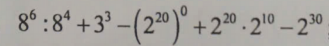
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LT
5
4 tháng 7 2016
Với a chữ số 2 và phép toán lũy thừa, số lớn nhất là : 2.2.2.2 = 24 = 16
4 tháng 7 2016
Số lớn nhất được tạo bởi 4 chữ số 2 và phép toán lũy thừa là: 2 x 2 x 2 x 2 = 24 = 16
Ủng hộ mk nha ^_-
DM
1
T
2
22 tháng 11 2021
Nâng lên lũy thừa, hay sự mũ hóa, là quá trình nhân một giá trị của cơ số b với chính nó với số lần cho trước bởi số mũ n thành số hạng b^n. thì lũy thừa mới của b là tích của n nhân với m. ... tuy nhiên số bất kỳ nâng lên lũy thừa 0 đều bằng 1 miễn là giá trị của cơ số của nó không phải là 0.
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ.
Ví dụ: \(3^{11}:3^9=3^{11-9}=3.3=9\)
chú ý : Mọi số tự nhiên đều viết được dưới dạng tổng các lũy thừa của 10
HT
TD
22 tháng 11 2021
I. Phép nâng lên lũy thừa
Lũy thừa bậc n của a , kí hiệu an , là tích của n thừa số a :
an = a . a . ... . a với n ∈ N*
n thừa số
Số a được gọi là cơ số, n được gọi là số mũ
VD: 2 . 2 . 2 . 2 . 2 . 2 = 26
Quy ước: a1 = a
a2 còn được gọi là "a bình phương" hay "bình phương của a"
a3 còn được gọi là "a chính phương" hay "chính phương của a"
*Với n là số tự nhiên khác 0, ta có:
10n = 1 0 ... 0.
n chữ số 0
NH
4
10 tháng 11 2019
72015 = 72012 . 73 = 74 . 503 . ...3 = ...1 . ...3 = ...3
Suy ra 72015 có chữ số tận cùng là 3
26 tháng 10 2014
tương tự câu này bạn ơi bạn đọc và làm bài của mình nhé
S=1+2+22+....+22012
A.2 =2+22+23+.........+22013
A.2-A=22013-1
A=22013-1
Ta thấy: 22013-1 < 22013
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 3 2022
\(P=n^3+7n^2+25n+39=\left(n+3\right)\left(n^2+4n+13\right)\)
Hiển nhiên \(\left\{{}\begin{matrix}n+3>1\\n^2+4n+13>1\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}n+3=p^a\\n^2+4n+13=p^b\end{matrix}\right.\) với \(b>a>0\)
\(\Rightarrow\left\{{}\begin{matrix}n+3⋮p\\n^2+4n+13⋮p\end{matrix}\right.\) \(\Rightarrow n^2+4n+13-\left(n+3\right)\left(n+1\right)⋮p\)
\(\Rightarrow10⋮p\Rightarrow\left[{}\begin{matrix}p=2\\p=5\end{matrix}\right.\)
- TH1: \(p=2\Rightarrow n+3=2^a\)
Do n nguyên dương \(\Rightarrow n+3\ge4\Rightarrow a\ge2\Rightarrow2^a⋮4\)
\(\Rightarrow n+3⋮4\Rightarrow n=4k+1\)
Đồng thời \(n^2+4n+13=2^b\), hiển nhiên \(b>2\Rightarrow n^2+4n+13⋮4\)
\(\Rightarrow\left(4k+1\right)^2+4\left(4k+1\right)+13⋮4\)
\(\Rightarrow4k\left(4k+6\right)+18⋮4\) (vô lý)
\(\Rightarrow p=2\) không thỏa mãn
TH2: \(p=5\) \(\Rightarrow\left\{{}\begin{matrix}n+3=5^a\\n^2+4n+13=5^b\end{matrix}\right.\)
\(\Rightarrow\left(n+1\right)\left(n+3\right)+10=5^b\)
\(\Rightarrow5^a\left(5^a-2\right)+10=5^b\)
\(\Rightarrow5^{a-1}\left(5^a-2\right)+2=5^{b-1}\)
- Với \(a=1\Rightarrow b=2\)
- Với \(a>1\Rightarrow\) vế trái chia 5 dư 2, vế phải chia hết cho 5
\(\Rightarrow\) Không tồn tại a;b nguyên thỏa mãn
Vậy \(a=1\Rightarrow n=5^1-3=2\)
\(=8^{6-4}+3^3-1+2^{20+10}-2^{30}\)
\(=8^2+3^3-1+2^{30}-2^{30}\)
\(=8^2+3^3-1\)
\(=64+27-1\)
\(=90\)