Chứng minh rằng bốn trung điểm của bốn cạnh hình thoi cùng thuộc một đường tròn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


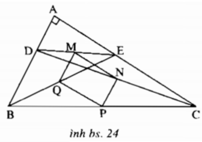
Xét ΔCDB có CN/CD=CP/CB
nên NP//BD và NP=DB/2
Xét ΔEDB có EM/ED=EQ/EB
nên MQ//BD và MQ=BD/2
=>NP//MQ và NP=MQ
Xét ΔDEC có DN/DC=DM/DE
nên MN//EC
=>MN vuông góc với AB
=>MN vuông góc với NP
Xét tứ giác MNPQ có
NP//MQ
NP=MQ
MN vuông góc với NP
Do đó: MNPQ là hình chữ nhật
=>M,N,P,Q cùng thuộc 1 đường tròn

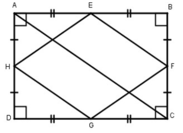
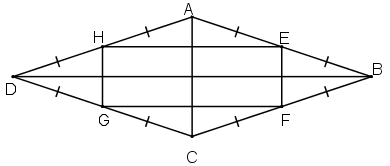
Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA của hình chữ nhật ABCD.
Kẻ đường chéo AC, BD
* Trong ∆ ABC, ta có:
E là trung điểm của AB
F là trung điểm của BC
Nên EF là đường trung bình của ∆ ABC.
⇒ EF // AC và EF = 1/2 AC (t/chất đường trung bình của tam giác) (1)
Trong ∆ ADC, ta có: H là trung điểm của AD
G là trung điểm của DC
Nên HG là đường trung bình của tam giác ADC.
⇒ HG // AC và HG = 1/2 AC (t/chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
Xét ∆ AEH và ∆ DGH, ta có: AH = HD (gt)
∠ EAH và ∠ GDH = 90 °
AE = DG (vì AB = CD)
Suy ra: ∆ AEH = ∆ DGH (c.g.c) ⇒ HE = HG
Vậy hình bình hành EFGH là hình thoi (hình bình hành có 2 cạnh kề bằng nhau).

Tham khảo:
Xét tam giác DEC có
M là trung điểm DE
N là trung điểm DC
MN là đường trung bình của tam giác DEC, hay MN//EC (*) và MN=1/2 EC (1)
* Xét tam giác BEC có
Q là trung điểm BE
P là trung điểm BC
PQ là đường trung bình của tam giác BEC, hay PQ//EC và PQ=1/2 EC (2).
Từ (1) và (2) suy ra tứ giác MNPQ là hình bình hành.
* Xét tam giác DEB có
Q là trung điểm BE
M là trung điểm DE
QM là đường trung bình của tam giác BED, hay MQ//DB (3).
Mà AB⊥AC (4)
Từ (1), (3) và (4) suy ra MN⊥MQ (5)
Tứ giác MNPQ là hình bình hành mà có một góc vuông MNPQ là hình chữ nhật.
Gọi I là giao điểm của hai đường chéo MP và QN
Suy ra IM=IN=IP=IQ (tính chất hình chữ nhật)
Nên các điểm M, N, P, Q đều cách đều I một khoảng cố định
M, N, P, Q cùng thuộc một đường tròn.

Gọi ABCD là hình chữ nhật
M,N,P,Q là trung điểm 4 canh AB,BC,CD,DA
Kẻ đường chéo AC ,BD
Xét tam giác ABC,ta có M,N là đường trugn binh của tam giác ABC
=> MN //= 1/2 AC (1)
Chưng minh tương tự với tam giác ACD => PQ//= 1/2 AC (2)
Tam giac ABD có MQ là đường trung binh => MQ //=1/2 BD (3)
Tam giác BDC có NP là đương trung binh => NP //=1/2 BD (4)
tỪ (1),(2),(3),(4) có AC=BD (đương chéo chữ nhật)=>MN =NP=PQ=QM
Hay MNPQ là hinh thoi
chung minh rang cac trung diem cua 4 canh cua 1 hcn là các đỉnh cua hình thoi

Tham khảo: https://loigiaihay.com/bai-75-trang-106-sgk-toan-8-tap-1-c43a3348.html
* Xét tam giác ABC có E và F lần lượt là trung điểm của AB và BC
=> EF là đường trung bình của tam giác ABC
* Tương tự tam giác ADC có HG là đường trung bình nên:
Từ (1) và (2) suy ra: EF // HG và EF = HG
=> tứ giác EFGH là hình bình hành.
Lại có: EF // AC và BD ⊥ AC nên BD ⊥ EF
EH // BD và EF ⊥ BD nên EF ⊥ EH
Nên
Hình bình hành EFGH có Ê = 90º nên là hình chữ nhật

Tham kho dưới đây nhé
https://loigiaihay.com/bai-75-trang-106-sgk-toan-8-tap-1-c43a3348.html
Xét hcn ABCD có M,N,P,Q là trung điểm AB,BC,CD,DA
Ta thấy MN,PQ lần lượt là đường trung bình tam giác ABC và ACD
Suy ra MN//AC;\(MN=\dfrac{1}{2}AC\) và PQ//AC;\(PQ=\dfrac{1}{2}AC\)
Do đó MN//PQ và MN=PQ
Hay MNPQ là hbh
Lại có NP là đtb tg BCD nên \(NP=\dfrac{1}{2}BD\)
Mà ABCD là hcn nên \(NP=\dfrac{1}{2}BD=\dfrac{1}{2}AC=MN\)
Vậy MNPQ là hthoi (đpcm)

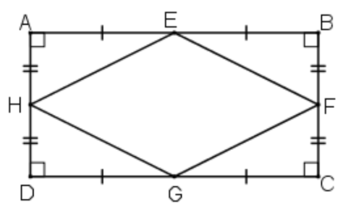
* Xét tam giác ABD có E và H lần lượt là trung điểm của AB và AD
=> EH là đường trung bình của tam giác
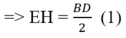
* Chứng minh tương tự, ta có:
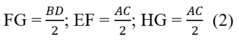
* Lại có, ABCD là hình chữ nhật nên AC = BD (3)
Từ (1), (2), (3) suy ra: EF = FG = GH= HE
=> tứ giác EFGH là hình thoi.

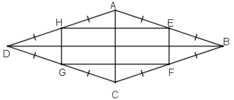
* Xét tam giác ABC có E và F lần lượt là trung điểm của AB và BC
=> EF là đường trung bình của tam giác ABC
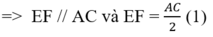
* Tương tự tam giác ADC có HG là đường trung bình nên:
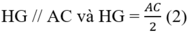
Từ (1) và (2) suy ra: EF // HG và EF = HG
=> tứ giác EFGH là hình bình hành.
Lại có: EF // AC và BD ⊥ AC nên BD ⊥ EF
EH // BD và EF ⊥ BD nên EF ⊥ EH
Nên 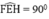
Hình bình hành EFGH có Ê = 90º nên là hình chữ nhật

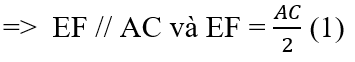
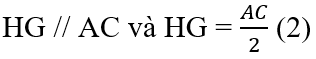
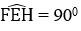
mày đao à