K
Khách
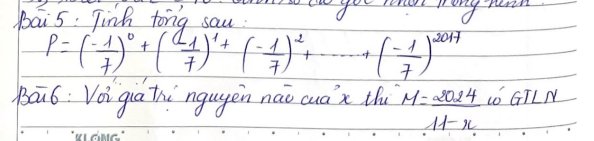
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BA
28 tháng 12 2020
Input: dãy số nguyên gồm n số được nhập từ bạn phím
Output: số lớn nhất, bé nhất trong dãy
BA
28 tháng 12 2020
B1: nhập dãy số nguyên
B2: gán max:=a[1]; min:=a[1]
B3: nếu max<a[i] thì max:=a[i]; min>a[i] then min:=a[i]
B4: in kết quả ra màn hình
31 tháng 10 2021
#include <bits/stdc++.h>
using namespace std;
double x,t;
int n,i;
int main()
{
cin>>n;
t=0;
for (i=1; i<=n; i++)
{
cin>>x;
t=t+x;
}
cout<<"tong cac so la:"<<fixed<<setprecision(2)<<t<<endl;
cout<<"trung binh la:"<<fixed<<setprecision(2)<<t/(n*1.0);
return 0;
}
24 tháng 10 2021
c: include <bits/stdc++.h>
using namespace std;
long long a,b,c;
int main()
{
cin>>a>>b>>c;
cout<<max(a,max(b,c));
return 0;
}
NQ
1
17 tháng 12 2016
Ta có 3x^2-x+1=3x^2+2x-3x-2+3=(3x-2)(x-1)+3
D có giá trị nguyên\(\) khi 3\(⋮\)(3x+2)\(\Leftrightarrow\)3x+2 là ước của 3\(\Leftrightarrow\)3x+2\(\in\){-3;-1;1;3} suy ra x\(\in\){-5/3;-1;-1/3;1/3}mà x nguyên nên ta tìm được x=-1
16 tháng 8 2022
Input: số nguyên n, dãy số nguyên A, số nguyên k
Output: số lượng phần tử có giá trị lớn hơn k
Thuật toán:
B1: Nhập N, dãy số nguyên A, số nguyên k
B2: dem←0; i←1;
B3: Nếu i>N thì chuyển đến B6.
B4: Nếu A[i]>k thì dem←dem+1
B5: i←i+1; Quay lại B3.
B6: In dem ra màn hình và kết thúc.
dem=0; i=1;
i>N (Sai): A[1] không lớn hơn k, i=i+1=2
i>N (Sai): A[2] lớn hơn k, dem=dem+1=1; i=i+1=3
i>N (Sai): A[3] không lớn hơn k; i=i+1=4
i>N (Sai): A[4] không lớn hơn k, i=i+1=5
i>N (Sai): A[5] lớn hơn k, dem=dem+1=2; i=i+1=6
i>N (Đúng): In dem là 6.
End
23 tháng 5 2022
uses crt;
var a:array[1..100]of integer;
i,n,nn,s:integer;
begin
clrscr;
readln(n);
for i:=1 to n do readln(a[i]);
nn:=a[1];
s:=1;
for i:=1 to n do
begin
if nn>a[i] then nn:=a[i];
s:=s*a[i];
end;
writeln(nn);
writeln(s);
readln;
end.
25 tháng 10 2021
#include <bits/stdc++.h>
using namespace std;
long long n,i,x,dem;
int main()
{
cin>>n;
dem=0;
for (i=1; i<=n; i++)
{
cin>>x;
if (x==50) dem++;
}
cout<<dem;
return 0;
}
27 tháng 10 2021
a: #incldue <bits/stdc++.h>
using namespace std;
long long i,n,x,t;
int main()
{
cin>>n;
t=0;
for (i=1; i<=n; i++)
{
cin>>x;
if (x>0) t=t+x;
}
cout<<t;
return 0;
}
\(P=\left(-\dfrac{1}{7}\right)^0+\left(-\dfrac{1}{7}\right)^1+\left(-\dfrac{1}{7}\right)^2+...+\left(-\dfrac{1}{7}\right)^{2017}\)
\(\left(-\dfrac{1}{7}\right).P=\left(-\dfrac{1}{7}\right)^1+\left(-\dfrac{1}{7}\right)^2+...+\left(-\dfrac{1}{7}\right)^{2017}+\left(-\dfrac{1}{7}\right)^{2018}\)
\(P-\left(-\dfrac{1}{7}\right)P=\left(-\dfrac{1}{7}\right)^0-\left(-\dfrac{1}{7}\right)^{2018}\)
\(\dfrac{8}{7}P=1-\dfrac{1}{7^{2018}}\)
\(\dfrac{8}{7}P=\dfrac{7^{2018}-1}{7^{2018}}\)
\(P=\dfrac{7^{2018}-1}{8.7^{2017}}\)