giải bài tập toán : thu gọn biểu thức :A=(x-1)^2+(x+1)^2-(x-1)(x+1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


=> B= (x-1)(x^2-x+1).2(x+1)3(x^2+x+1)
=> B= 6(x-1)(x^2+x+1).(x+1)(x^2-x+1)
=>B =6(x^3-1)(x^3+1)
=> B 6x^6-6

Bài 4:
b: \(=x^2z\left(-1+3-7\right)=-5x^2z=-5\cdot\left(-1\right)^2\cdot\left(-2\right)=10\)
c: \(=xy^2\left(5+0.5-3\right)=2.5xy^2=2.5\cdot2\cdot1^2=5\)

a.ta có
\(\left(x+3\right)^3+\left(x^2+1\right)\left(x-2\right)=x^3+9x^2+27x+27+x^3-2x^2+x-2\)
\(=2x^3+7x^2+28x+25\)
b.\(\left(2x-1\right)^2-\left(2-x\right)^3=4x^2-4x+1+x^3-6x^2+12x-8\)
\(=x^3-2x^2+8x-7\)
a) (x + 3)3 + (x2 + 1)(x - 2)
= x3 + 9x2 + 27x + 27 + x3 - 2x + x - 2
= x3 + x3 + 9x2 + 27x - 2x + x + 27 - 2
= 2x3 + 9x2 + 26x + 25
b) (2x - 1)2 - (2 - x)3
= 4x2 - 4x + 1 - ( 8 - 12x + 6x2 - x3)
= 4x2 - 4x + 1 - 8 + 12x - 6x2 + x3
= x3 + 4x2 - 6x2 + 12x - 4x + 1 - 8
= x3 - 2x2 + 8x - 7

\(a,B=4\sqrt{x=1}-3\sqrt{x+1}+2\)\(\sqrt{x+1}+\sqrt{x+1}\)
\(=4\sqrt{x+1}\)
\(b,\)đưa về \(\sqrt{x+1}=4\Rightarrow x=15\)
a, Với \(x\ge-1\)
\(\Rightarrow B=4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}\)
\(=4\sqrt{x+1}\)
b, Ta có B = 16 hay
\(4\sqrt{x+1}=16\Leftrightarrow\sqrt{x+1}=4\)bình phương 2 vế ta được
\(\Leftrightarrow x+1=16\Leftrightarrow x=15\)

a: ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)
b: Ta có: \(A=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)
\(=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{2}{x+\sqrt{x}+1}\)
c: Ta có: \(x+\sqrt{x}+1>0\forall x\) thỏa mãn ĐKXĐ
\(\Leftrightarrow\dfrac{2}{x+\sqrt{x}+1}>0\forall x\)

a) x(x + 1) - 2x(x - 2) = x2 + x - 2x2 + 4x = -x2 + 5x
b) -3x(x - 1) + (x - 1)(x + 1) = -3x2 + 3x + x2 - 1 = -2x2 + 3x - 1
c) (3x - 2)(3x + 2) - (x - 1)(x + 2) = 9x2 - 4 - x2 - x + 2
= 8x2 - x - 2
a, x(x+1) - 2x(x -2 )
= x2 +x - 2x2 + 4x = -x2 + 5x
b, -3x( x - 1 ) + ( x -1 ) ( x+1 )
= -3x2 + 3x + x2 -1
= -2x2 + 3x -1
c, ( 3x-2 ) ( 3x + 2 ) - ( x -1 ) ( x +2 )
= 9x2 - 4 - ( x2 + 2x -x -2 )
= 9x2 -4 - x2 -2x + x + 2
= 8x2 -x -2
*Sxl

Bài 5:
\(x^3=18+3\sqrt[3]{\left(9+4\sqrt{5}\right)\left(9-4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\\ \Leftrightarrow x^3=18+3x\sqrt[3]{1}\\ \Leftrightarrow x^3-3x=18\\ y^3=6+3\sqrt[3]{\left(3-2\sqrt{2}\right)\left(3+2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\\ \Leftrightarrow y^3=6+3y\sqrt[3]{1}\\ \Leftrightarrow y^3-3y=6\\ P=x^3+y^3-3\left(x+y\right)+1993\\ P=\left(x^3-3x\right)+\left(y^3-3y\right)+1993\\ P=18+6+1993=2017\)

a: \(=9-4\sqrt{5}\cdot\dfrac{1}{\sqrt{5}}=9-4=5\)
b: \(=\sqrt{5}-2-\dfrac{1}{2}\cdot2\sqrt{5}=-2\)
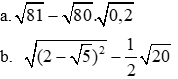
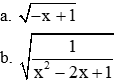
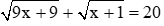
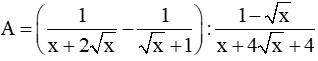
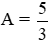
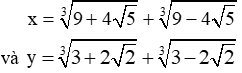
\(A=\left(x-1\right)^2+\left(x+1\right)^2-\left(x-1\right).\left(x+1\right)=x^2-2x+1+x^2+2x+1-x^2-1=x^2-1\)